问Python的eval()会忽略不连续性？

EN

COMPUTATION_DISTANCE = 0.001
# THE DISTANCE BETWEEN EACH X VALUE WHEN PLOTTING POINTS. EVENTUALLY WE CONNECT A LINE BETWEEN ALL POINTS SEPERATED BY A VALUE OF COMPUTATION_DISTANCE.
# IF THE GRAPH IS ZOOMED,  MULTIPLY THIS COMPUTATION DISTANCE BY A FACTOR OF THAT ZOOM
ASYMPTOTE = 2.0

#formula = "(x+2)**2" #just a fake formula to begin
formula = "(x-2)/((x**2)-4)" #just a fake formula to begin
view_size = 8.0




    def draw_graph(event):
        global alreadyGraphedDeriv #to prevent infinite loop of graphing deriv
        alreadyGraphedDeriv = False
        canvas.delete("all") #clear existing graph
        draw_grid()
        y_previous = 0.0
        x = view_size * -1 #start at the negative of the view_size. so x =-8. then the loop wil keep repeating until x =+8 giving u all the x values. the loop takes care of the y values
        while x <= view_size:
            try: 
                y = eval(formula) #evaluate y at every point x
                print(str(x) + ", " + str(y))
                #if(y>1000000000000 or y < 1000000000000): #finding asymptotes
                    #print("Asymptote at (" + str(x) + ", " + str(y) + ") ")

            except ValueError:
                y = 1000000000
                x = COMPUTATION_DISTANCE * view_size
                print('Value error')
                if eval(formula) < 0:
                    y *= -1
            except:
                print_formula("SYNTAX ERROR   ")
                print("syntax error")
                break
            try:
                draw_line(x - COMPUTATION_DISTANCE * view_size, y_previous, x, y, "black") #(previous x, previous y, new x, new y, color)
            except:
                print_formula("NON-INT PWR (dbl click ^)   ")
                break
            y_previous = y
            x += COMPUTATION_DISTANCE * view_size
            #print(" " + str(x - COMPUTATION_DISTANCE * view_size) + " " + str(y_previous) + " " + str(x) + " " + str(y) +  " black") 
            #(previous x, previous y, new x, new y, color)

        if alreadyGraphedDeriv is False:
            alreadyGraphedDeriv = True
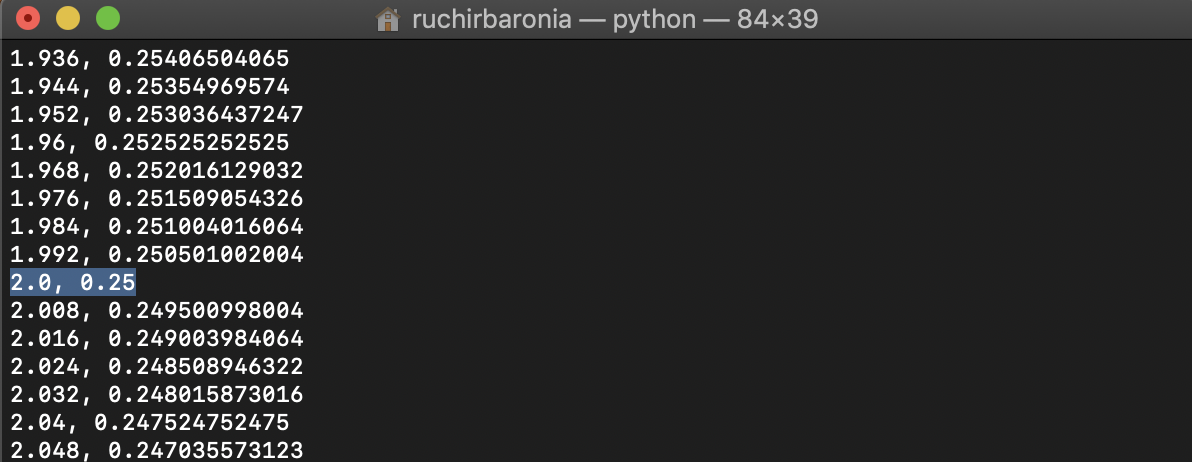
            draw_derivative("event")