《算法导论》第 4 章 - 分治策略
《算法导论》第 4 章 - 分治策略

啊阿狸不会拉杆
发布于 2026-01-21 13:00:15
发布于 2026-01-21 13:00:15
引言
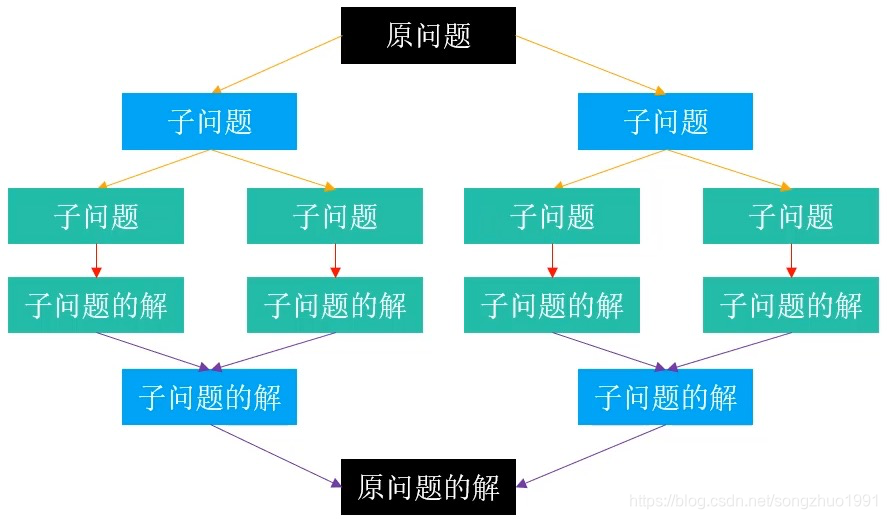
分治策略(Divide and Conquer)是算法设计中的一种重要思想,其核心思想是将一个复杂问题分解为若干个规模较小的子问题,递归地解决这些子问题,然后将子问题的解合并,从而得到原问题的解。分治策略在许多高效算法中都有应用,如快速排序、归并排序、Strassen 矩阵乘法等。

本章将详细讲解《算法导论》第 4 章关于分治策略的内容,包括经典问题、算法设计、递归式求解方法等,并通过完整的 C++ 代码实现帮助读者深入理解和实践。
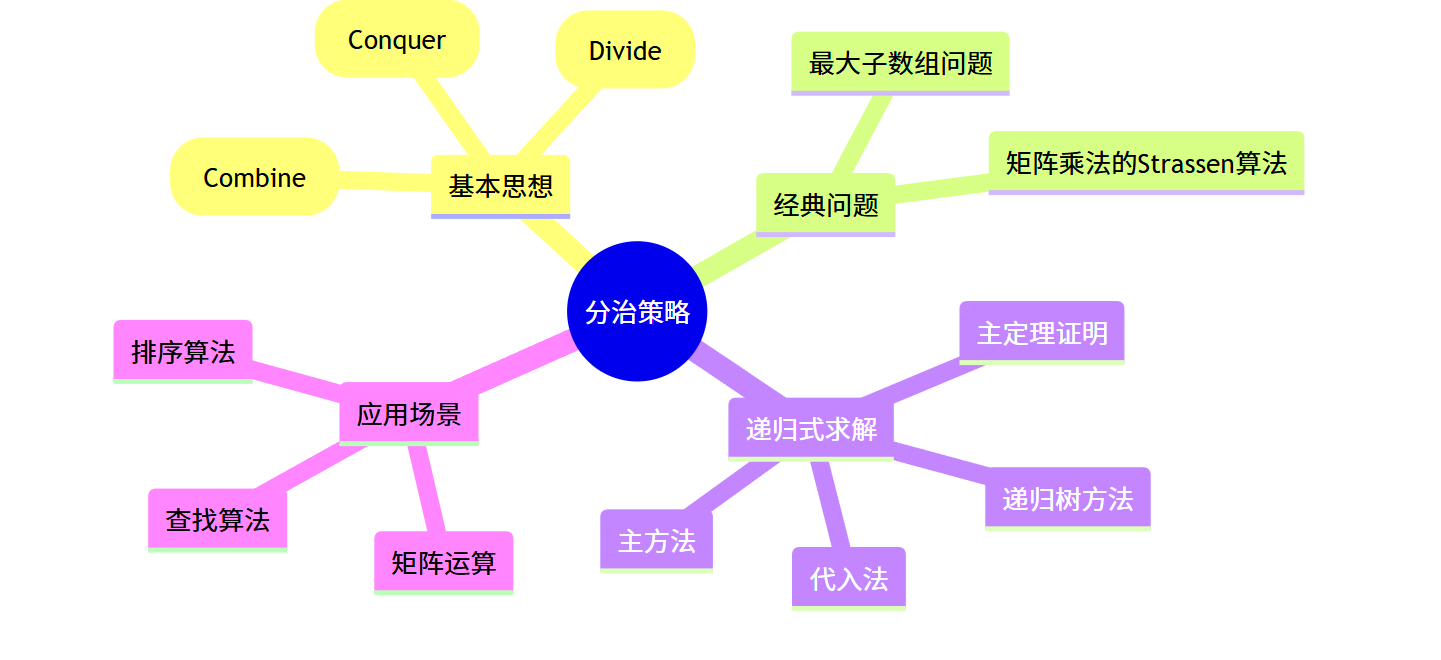
思维导图
4.1 最大子数组问题
问题定义
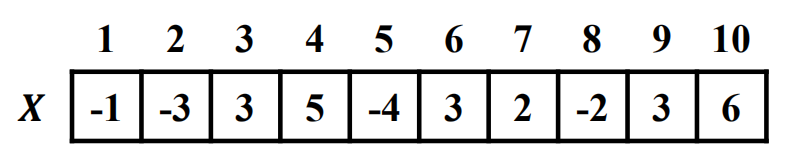
最大子数组问题(Maximum Subarray Problem)是指:给定一个整数数组,找到一个具有最大和的连续子数组(至少包含一个元素),返回其最大和。
例如,对于数组 [-2, 1, -3, 4, -1, 2, 1, -5, 4],其最大子数组是 [4, -1, 2, 1],最大和为 6。
分治思路
使用分治策略解决最大子数组问题的步骤如下:
- 分解:将数组从中间分成左右两个子数组。
- 解决:递归地求解左右两个子数组的最大子数组。
- 合并:求出跨越中间点的最大子数组,然后与左右子数组的最大子数组比较,取最大者作为原数组的最大子数组。
其中,跨越中间点的最大子数组求解是关键,需要分别从中间点向左、向右寻找最大子数组,然后合并这两个子数组。
流程图
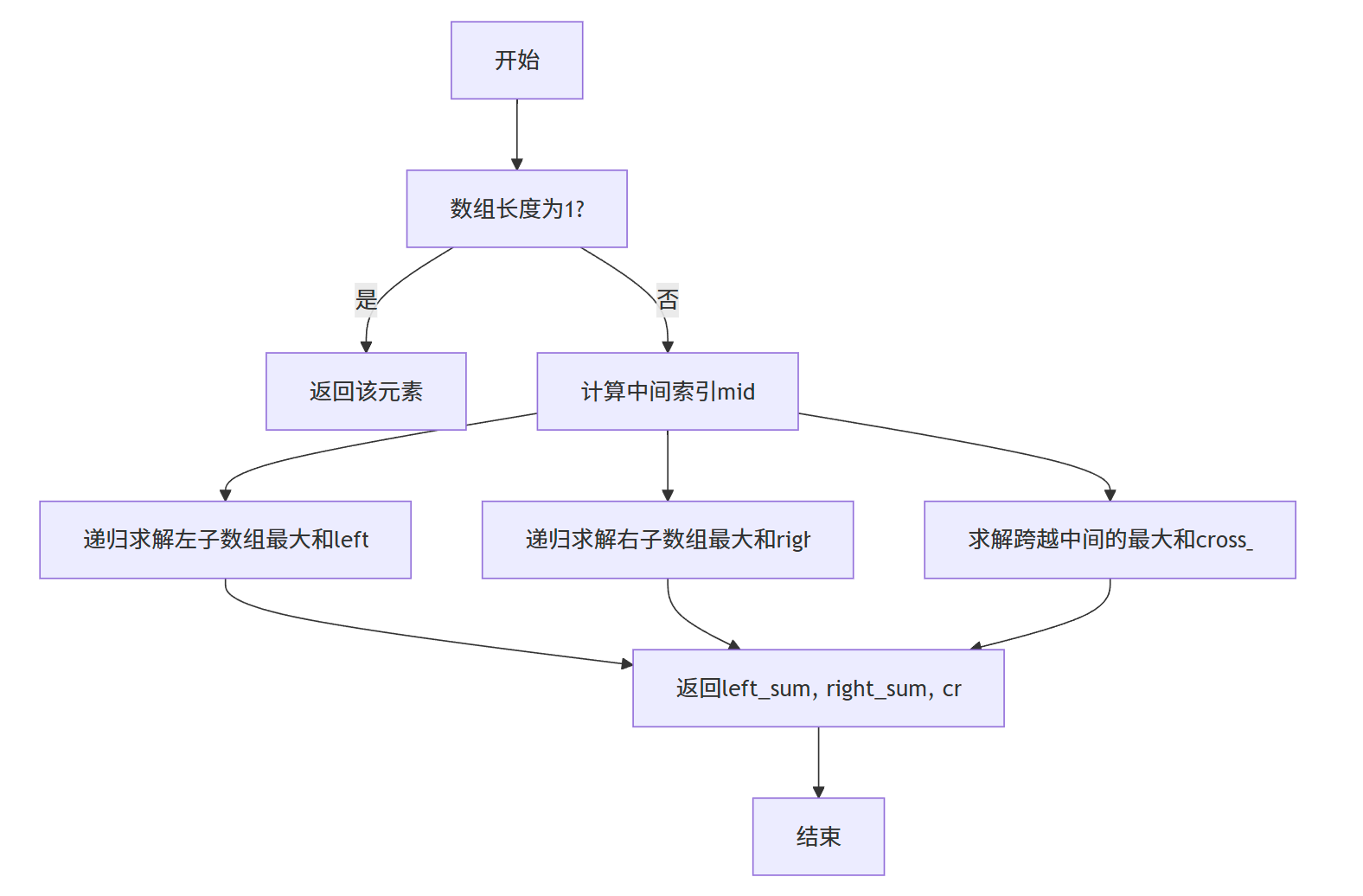
代码实现
#include <iostream>
#include <vector>
#include <climits> // 用于INT_MIN
#include <algorithm> // 用于max函数
using namespace std;
/**
* 计算跨越中间点的最大子数组和
* @param nums 输入数组
* @param left 左边界索引
* @param mid 中间索引
* @param right 右边界索引
* @return 跨越中间点的最大子数组和
*/
int maxCrossingSubarray(const vector<int>& nums, int left, int mid, int right) {
// 计算左半部分(从mid向左)的最大和
int left_sum = INT_MIN;
int sum = 0;
for (int i = mid; i >= left; --i) {
sum += nums[i];
if (sum > left_sum) {
left_sum = sum;
}
}
// 计算右半部分(从mid+1向右)的最大和
int right_sum = INT_MIN;
sum = 0;
for (int i = mid + 1; i <= right; ++i) {
sum += nums[i];
if (sum > right_sum) {
right_sum = sum;
}
}
// 返回左右两部分的和(跨越中间点)
return left_sum + right_sum;
}
/**
* 递归求解最大子数组和
* @param nums 输入数组
* @param left 左边界索引
* @param right 右边界索引
* @return 最大子数组和
*/
int maxSubarrayRecursive(const vector<int>& nums, int left, int right) {
// 基本情况:数组只有一个元素
if (left == right) {
return nums[left];
}
// 计算中间索引
int mid = (left + right) / 2;
// 递归求解左子数组、右子数组的最大和
int left_sum = maxSubarrayRecursive(nums, left, mid);
int right_sum = maxSubarrayRecursive(nums, mid + 1, right);
// 求解跨越中间的最大和
int cross_sum = maxCrossingSubarray(nums, left, mid, right);
// 返回三者中的最大值
return max({left_sum, right_sum, cross_sum});
}
/**
* 最大子数组问题的分治解法
* @param nums 输入数组
* @return 最大子数组和
*/
int maxSubArray(const vector<int>& nums) {
if (nums.empty()) {
throw invalid_argument("数组不能为空");
}
return maxSubarrayRecursive(nums, 0, nums.size() - 1);
}
// 测试函数
int main() {
vector<int> nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
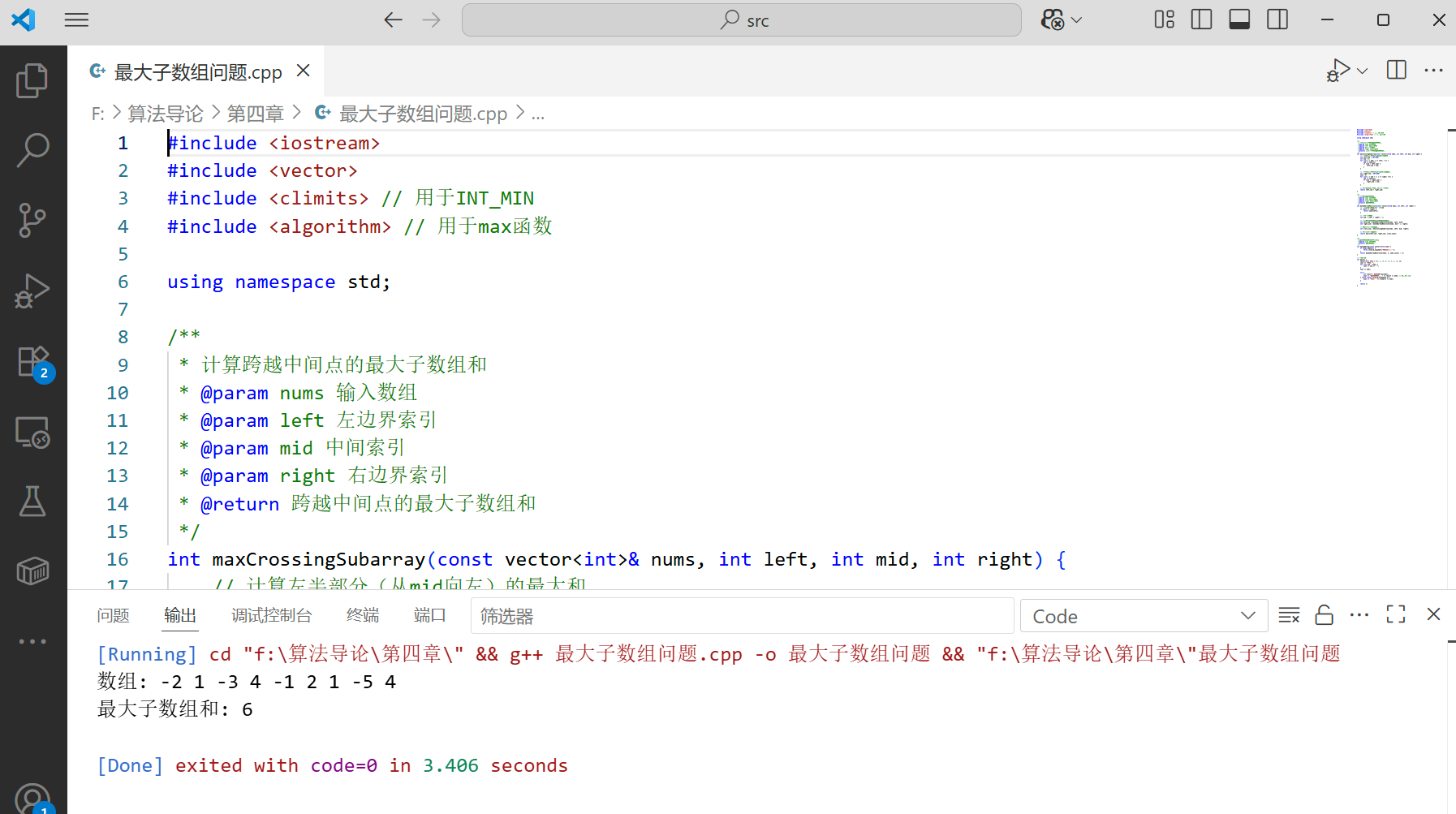
cout << "数组: ";
for (int num : nums) {
cout << num << " ";
}
cout << endl;
try {
int result = maxSubArray(nums);
cout << "最大子数组和: " << result << endl; // 预期输出:6
} catch (const invalid_argument& e) {
cout << "错误: " << e.what() << endl;
}
return 0;
}
代码说明
maxCrossingSubarray函数:计算跨越中间点的最大子数组和,分别从中间点向左、向右累加,记录最大和。maxSubarrayRecursive函数:递归实现分治策略,分解问题并合并结果。maxSubArray函数:包装函数,处理边界情况并调用递归函数。- 时间复杂度:O (n log n),其中 n 是数组长度。递归树的深度为 O (log n),每层的合并操作(计算跨越中间的最大子数组)为 O (n)。
4.2 矩阵乘法的 Strassen 算法
问题背景
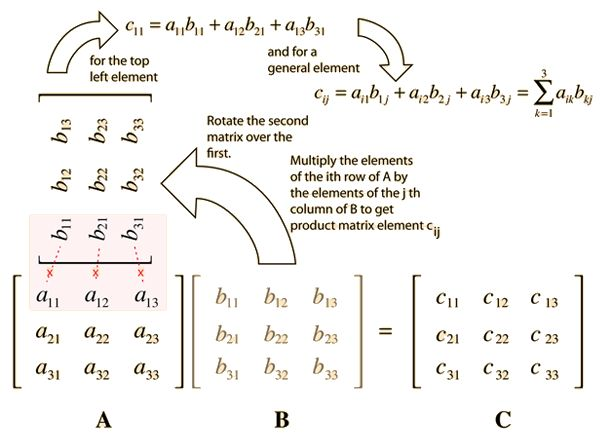
矩阵乘法是线性代数中的基本运算。对于两个 n×n 的矩阵 A 和 B,它们的乘积 C 也是一个 n×n 的矩阵,其中 C [i][j] = Σ(A [i][k] * B [k][j]) (k 从 1 到 n)。
普通矩阵乘法的时间复杂度为 O (n³),而 Strassen 算法通过分治策略将时间复杂度降低到了 O (n^log₂7) ≈ O (n²・⁸⁰⁷)。
Strassen 算法步骤
分解:将矩阵 A、B、C 各分解为 4 个 n/2×n/2 的子矩阵:
plaintext
A = [[A₁₁, A₁₂], B = [[B₁₁, B₁₂], C = [[C₁₁, C₁₂],
[A₂₁, A₂₂]] [B₂₁, B₂₂]] [C₂₁, C₂₂]]其中,C₁₁ = A₁₁B₁₁ + A₁₂B₂₁ C₁₂ = A₁₁B₁₂ + A₁₂B₂₂ C₂₁ = A₂₁B₁₁ + A₂₂B₂₁ C₂₂ = A₂₁B₁₂ + A₂₂B₂₂
计算 7 个中间矩阵:
- M₁ = (A₁₁ + A₂₂) * (B₁₁ + B₂₂)
- M₂ = (A₂₁ + A₂₂) * B₁₁
- M₃ = A₁₁ * (B₁₂ - B₂₂)
- M₄ = A₂₂ * (B₂₁ - B₁₁)
- M₅ = (A₁₁ + A₁₂) * B₂₂
- M₆ = (A₂₁ - A₁₁) * (B₁₁ + B₁₂)
- M₇ = (A₁₂ - A₂₂) * (B₂₁ + B₂₂)
计算 C 的子矩阵:
- C₁₁ = M₁ + M₄ - M₅ + M₇
- C₁₂ = M₃ + M₅
- C₂₁ = M₂ + M₄
- C₂₂ = M₁ - M₂ + M₃ + M₆
组合:将 C₁₁、C₁₂、C₂₁、C₂₂组合成矩阵 C。
代码实现
#include <iostream>
#include <vector>
#include <cmath> // 用于ceil函数
using namespace std;
// 定义矩阵类型
using Matrix = vector<vector<int>>;
/**
* 矩阵加法
* @param A 矩阵A
* @param B 矩阵B
* @return 矩阵A + B
*/
Matrix add(const Matrix& A, const Matrix& B) {
int n = A.size();
Matrix result(n, vector<int>(n));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
result[i][j] = A[i][j] + B[i][j];
}
}
return result;
}
/**
* 矩阵减法
* @param A 矩阵A
* @param B 矩阵B
* @return 矩阵A - B
*/
Matrix subtract(const Matrix& A, const Matrix& B) {
int n = A.size();
Matrix result(n, vector<int>(n));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
result[i][j] = A[i][j] - B[i][j];
}
}
return result;
}
/**
* 普通矩阵乘法(用于小矩阵或边界情况)
* @param A 矩阵A
* @param B 矩阵B
* @return 矩阵A * B
*/
Matrix multiplyNaive(const Matrix& A, const Matrix& B) {
int n = A.size();
Matrix result(n, vector<int>(n, 0));
for (int i = 0; i < n; ++i) {
for (int k = 0; k < n; ++k) {
if (A[i][k] != 0) { // 优化:跳过零元素
for (int j = 0; j < n; ++j) {
result[i][j] += A[i][k] * B[k][j];
}
}
}
}
return result;
}
/**
* 将大矩阵分割为4个子矩阵
* @param parent 父矩阵
* @param child 子矩阵(输出)
* @param row 子矩阵在父矩阵中的起始行(0或n/2)
* @param col 子矩阵在父矩阵中的起始列(0或n/2)
* @param n 子矩阵的大小
*/
void splitMatrix(const Matrix& parent, Matrix& child, int row, int col, int n) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
child[i][j] = parent[row + i][col + j];
}
}
}
/**
* 将4个子矩阵合并为大矩阵
* @param parent 父矩阵(输出)
* @param child 子矩阵
* @param row 子矩阵在父矩阵中的起始行(0或n/2)
* @param col 子矩阵在父矩阵中的起始列(0或n/2)
* @param n 子矩阵的大小
*/
void mergeMatrix(Matrix& parent, const Matrix& child, int row, int col, int n) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
parent[row + i][col + j] = child[i][j];
}
}
}
/**
* Strassen算法实现矩阵乘法
* @param A 矩阵A
* @param B 矩阵B
* @return 矩阵A * B
*/
Matrix strassenMultiply(const Matrix& A, const Matrix& B) {
int n = A.size();
// 基本情况:当矩阵大小较小时,使用普通乘法(效率更高)
if (n <= 64) { // 阈值可调整,通常取64或32
return multiplyNaive(A, B);
}
// 计算新的矩阵大小(确保是2的幂,便于分割)
int new_size = 1;
while (new_size < n) {
new_size <<= 1; // 等价于new_size *= 2
}
// 补全矩阵为new_size x new_size(不足部分补0)
Matrix A_padded(new_size, vector<int>(new_size, 0));
Matrix B_padded(new_size, vector<int>(new_size, 0));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
A_padded[i][j] = A[i][j];
B_padded[i][j] = B[i][j];
}
}
// 分割矩阵为4个子矩阵
int half = new_size / 2;
Matrix A11(half, vector<int>(half));
Matrix A12(half, vector<int>(half));
Matrix A21(half, vector<int>(half));
Matrix A22(half, vector<int>(half));
Matrix B11(half, vector<int>(half));
Matrix B12(half, vector<int>(half));
Matrix B21(half, vector<int>(half));
Matrix B22(half, vector<int>(half));
splitMatrix(A_padded, A11, 0, 0, half);
splitMatrix(A_padded, A12, 0, half, half);
splitMatrix(A_padded, A21, half, 0, half);
splitMatrix(A_padded, A22, half, half, half);
splitMatrix(B_padded, B11, 0, 0, half);
splitMatrix(B_padded, B12, 0, half, half);
splitMatrix(B_padded, B21, half, 0, half);
splitMatrix(B_padded, B22, half, half, half);
// 计算7个中间矩阵
Matrix M1 = strassenMultiply(add(A11, A22), add(B11, B22));
Matrix M2 = strassenMultiply(add(A21, A22), B11);
Matrix M3 = strassenMultiply(A11, subtract(B12, B22));
Matrix M4 = strassenMultiply(A22, subtract(B21, B11));
Matrix M5 = strassenMultiply(add(A11, A12), B22);
Matrix M6 = strassenMultiply(subtract(A21, A11), add(B11, B12));
Matrix M7 = strassenMultiply(subtract(A12, A22), add(B21, B22));
// 计算C的4个子矩阵
Matrix C11 = add(subtract(add(M1, M4), M5), M7);
Matrix C12 = add(M3, M5);
Matrix C21 = add(M2, M4);
Matrix C22 = add(subtract(add(M1, M3), M2), M6);
// 合并子矩阵
Matrix C_padded(new_size, vector<int>(new_size));
mergeMatrix(C_padded, C11, 0, 0, half);
mergeMatrix(C_padded, C12, 0, half, half);
mergeMatrix(C_padded, C21, half, 0, half);
mergeMatrix(C_padded, C22, half, half, half);
// 截取结果为n x n矩阵(去除补全的部分)
Matrix C(n, vector<int>(n));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
C[i][j] = C_padded[i][j];
}
}
return C;
}
/**
* 打印矩阵
* @param mat 要打印的矩阵
*/
void printMatrix(const Matrix& mat) {
for (const auto& row : mat) {
for (int val : row) {
cout << val << "\t";
}
cout << endl;
}
}
// 测试函数
int main() {
// 测试用例:2x2矩阵乘法
Matrix A = {{1, 2},
{3, 4}};
Matrix B = {{5, 6},
{7, 8}};
cout << "矩阵A:" << endl;
printMatrix(A);
cout << endl << "矩阵B:" << endl;
printMatrix(B);
Matrix C_naive = multiplyNaive(A, B);
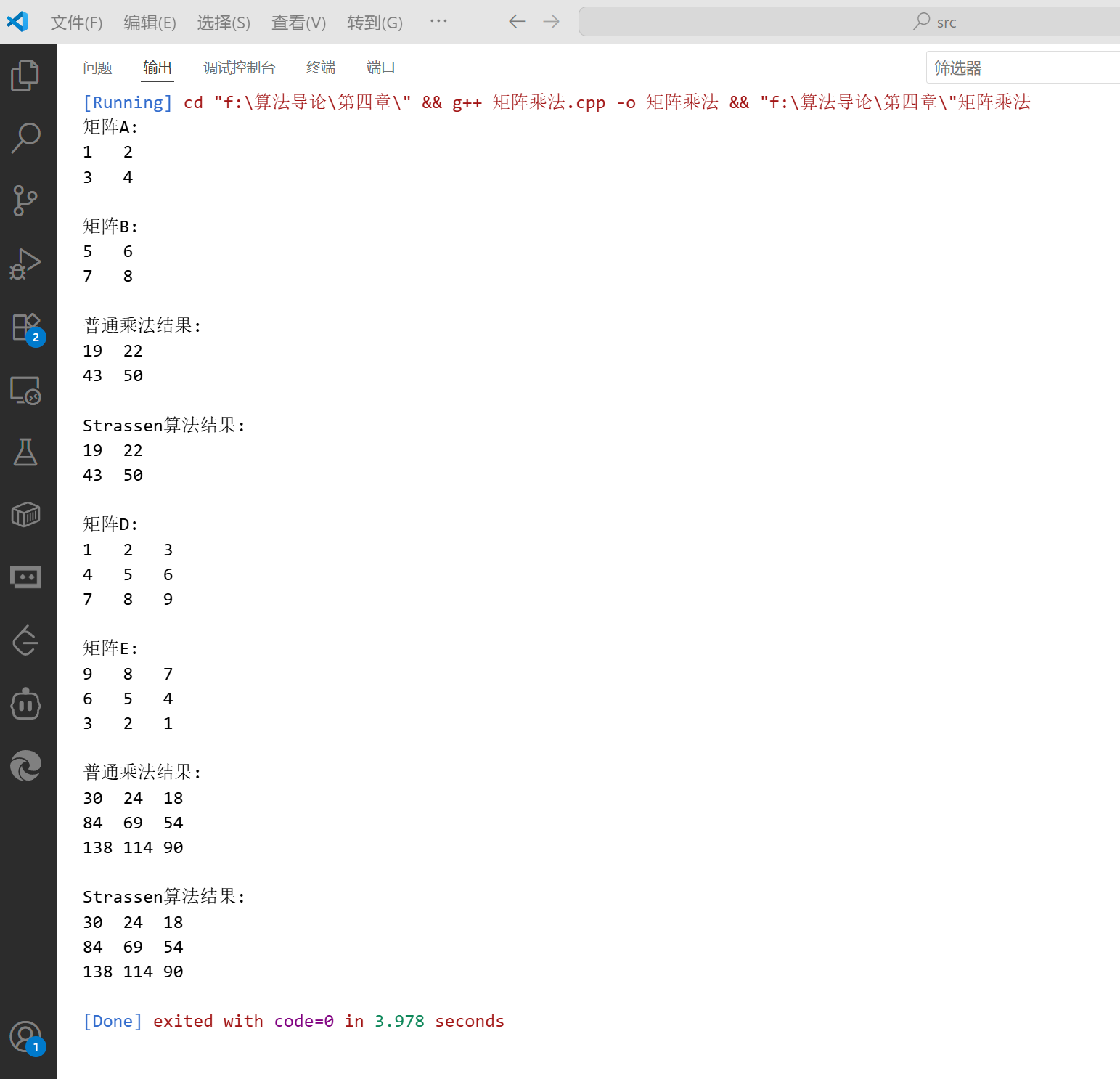
cout << endl << "普通乘法结果:" << endl;
printMatrix(C_naive);
Matrix C_strassen = strassenMultiply(A, B);
cout << endl << "Strassen算法结果:" << endl;
printMatrix(C_strassen);
// 测试用例:3x3矩阵乘法
Matrix D = {{1, 2, 3},
{4, 5, 6},
{7, 8, 9}};
Matrix E = {{9, 8, 7},
{6, 5, 4},
{3, 2, 1}};
cout << endl << "矩阵D:" << endl;
printMatrix(D);
cout << endl << "矩阵E:" << endl;
printMatrix(E);
Matrix F_naive = multiplyNaive(D, E);
cout << endl << "普通乘法结果:" << endl;
printMatrix(F_naive);
Matrix F_strassen = strassenMultiply(D, E);
cout << endl << "Strassen算法结果:" << endl;
printMatrix(F_strassen);
return 0;
}
代码说明
- 代码中实现了矩阵的加法、减法、普通乘法和 Strassen 乘法。
- 为了处理非 2 的幂大小的矩阵,代码中进行了补全操作(不足部分补 0)。
- 当矩阵大小较小时(如≤64),使用普通乘法效率更高,因此设置了阈值。
- Strassen 算法通过减少递归乘法的次数(7 次 vs 普通分治的 8 次)来降低时间复杂度。

4.3 用代入法求解递归式
方法概述
代入法(Substitution Method)是求解递归式的一种基本方法,其步骤如下:
- 猜测解的形式:根据递归式的结构,猜测解的渐近形式(如 T (n) = O (n log n))。
- 验证猜测:用数学归纳法证明猜测的解是正确的,即证明存在常数 c > 0 和 n₀,使得对于所有 n ≥ n₀,都有 T (n) ≤ c・g (n)(其中 g (n) 是猜测的解)。
示例解析
示例 1:求解递归式 T (n) = 2T (n/2) + n,其中 T (1) = 1。
- 猜测解:观察递归式,其形式与归并排序的递归式相同,猜测 T (n) = O (n log n)。
- 验证:
- 假设对于所有 k <n,有 T (k) ≤ c・k log k(归纳假设)。
- 对于 n,有: T (n) = 2T (n/2) + n ≤ 2·c·(n/2) log(n/2) + n = c·n (log n - log 2) + n = c·n log n - c·n + n ≤ c・n log n (当 c ≥ 1 时,-c・n + n ≤ 0)
- 因此,T (n) = O (n log n) 得证。
示例 2:求解递归式 T (n) = T (n/2) + T (n/4) + n,其中 T (1) = 1。
- 猜测解:猜测 T (n) = O (n)。
- 验证:
- 假设对于所有 k <n,有 T (k) ≤ c・k(归纳假设)。
- 对于 n,有: T (n) = T (n/2) + T (n/4) + n ≤ c·(n/2) + c·(n/4) + n = (3c/4)·n + n = n·(3c/4 + 1) ≤ c・n (当 c ≥ 4 时,3c/4 + 1 ≤ c)
- 因此,T (n) = O (n) 得证。
关键技巧
- 猜测解时,可以参考类似的递归式(如主方法中的典型形式)。
- 若初始猜测不成立,可以调整猜测的形式(如增加低阶项)。
- 注意归纳基础的验证(如 n=1,2 等小值时是否满足条件)。
4.4 用递归树方法求解递归式
方法概述
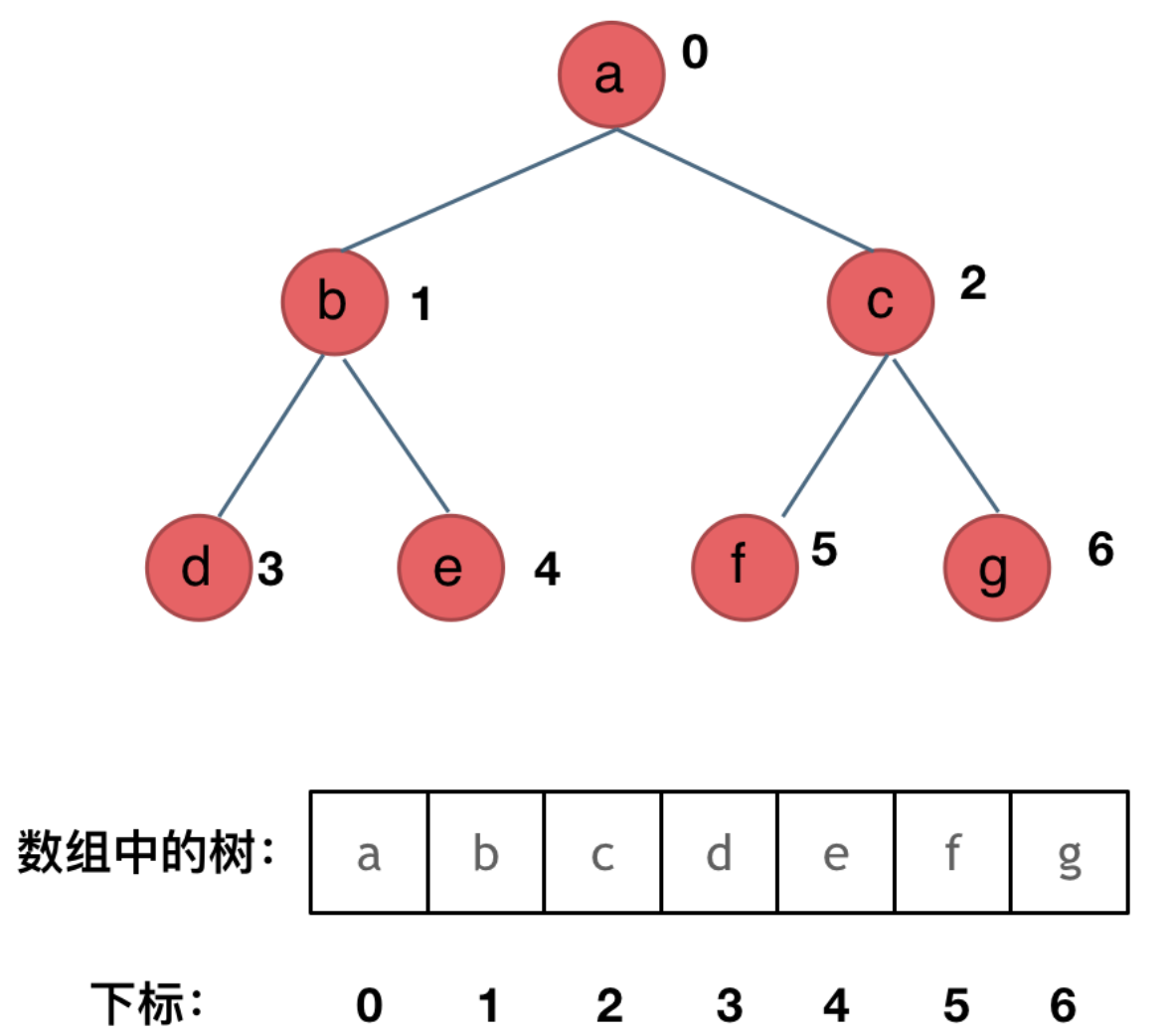
递归树(Recursion Tree)是一种可视化递归式的方法,通过将递归式展开为一棵树,每一层代表递归的一个层次,节点的值代表该层子问题的代价。求解步骤如下:
- 构建递归树:将递归式分解为树的形式,根节点是原问题的代价,子节点是子问题的代价。
- 计算每一层的代价:递归树的每一层对应递归的一个深度,计算该层所有节点的代价之和。
- 求和:将所有层的代价相加,得到递归式的解的渐近上界(或下界)。
示例解析
示例 1:求解递归式 T (n) = 3T (n/4) + n²。
- 构建递归树:
- 根节点:代价为 n²,有 3 个子节点(对应 3T (n/4))。
- 第 1 层:每个子节点的代价为 (n/4)²,共 3 个节点,总代价为 3・(n/4)²。
- 第 2 层:每个子节点的代价为 (n/16)²,共 3² 个节点,总代价为 3²・(n/16)²。
- ...
- 第 k 层:总代价为 3ᵏ・(n/4ᵏ)² = n²・(3/16)ᵏ。
- 确定树的深度:当 n/4ᵏ = 1 时,k = log₄n,因此树的深度为 log₄n。
- 求和: T(n) = n² + 3·(n/4)² + 3²·(n/16)² + ... + 3ᵏ·(n/4ᵏ)² = n²·[1 + (3/16) + (3/16)² + ... + (3/16)^log₄n] 这是一个等比数列,公比 r = 3/16 <1,无穷级数和为 1/(1 - r) = 16/13。 因此,T (n) = O (n²)。
示例 2:求解递归式 T (n) = T (n/3) + T (2n/3) + n。
- 构建递归树:
- 根节点:代价为 n,有 2 个子节点(T (n/3) 和 T (2n/3))。
- 第 1 层:代价分别为 n/3 和 2n/3,总代价为 n。
- 第 2 层:代价分别为 (n/3)/3, (n/3)・2/3, (2n/3)/3, (2n/3)・2/3,总代价为 n。
- ...
- 每一层的总代价均为 n。
- 确定树的深度:最右边的路径(每次乘以 2/3)最深,深度为 log₃/₂n = O (log n)。
- 求和: T(n) = n·O(log n) = O(n log n)。
流程图
4.5 用主方法求解递归式
方法概述
主方法(Master Method)适用于求解形如以下形式的递归式:
T(n) = aT(n/b) + f(n)
其中:
- a ≥ 1(子问题的数量)
- b > 1(每个子问题的规模是原问题的 1/b)
- f (n) 是渐近正函数(代表分解和合并的代价)
主方法通过比较 f (n) 与 n^log_b a 的大小关系,直接给出递归式的解:
- 情况 1:若 f (n) = O (n^log_b a - ε) 对于某个 ε > 0 成立,则 T (n) = Θ(n^log_b a)。
- 情况 2:若 f (n) = Θ(n^log_b a log^k n) 对于某个 k ≥ 0 成立,则 T (n) = Θ(n^log_b a log^{k+1} n)。
- 情况 3:若 f (n) = Ω(n^log_b a + ε) 对于某个 ε > 0 成立,且存在常数 c < 1 使得对于足够大的 n,有 a・f (n/b) ≤ c・f (n)(正则条件),则 T (n) = Θ(f (n))。
示例解析
示例 1:T(n) = 9T(n/3) + n
- a=9, b=3, log_b a = log₃9 = 2
- f (n) = n = O (n²⁻¹),满足情况 1
- 因此,T (n) = Θ(n²)
示例 2:T(n) = T(2n/3) + 1
- a=1, b=3/2, log_b a = 0
- f (n) = 1 = Θ(n⁰ log⁰ n),满足情况 2(k=0)
- 因此,T (n) = Θ(log n)
示例 3:T(n) = 3T(n/4) + n log n
- a=3, b=4, log_b a ≈ 0.793
- f (n) = n log n = Ω(n⁰・⁷⁹³ + ε)(取 ε=0.2),且验证正则条件: a・f (n/b) = 3・(n/4) log (n/4) ≤ 3/4・n log n ≤ c・f (n)(取 c=3/4 < 1)
- 满足情况 3,因此 T (n) = Θ(n log n)
示例 4:T(n) = 2T(n/2) + n log n
- a=2, b=2, log_b a = 1
- f (n) = n log n = Θ(n¹ log¹ n),满足情况 2(k=1)
- 因此,T (n) = Θ(n log² n)
注意事项
- 主方法的三种情况是互斥的,并非所有递归式都能适用主方法。
- 情况 3 中的正则条件是必要的,若不满足则无法应用情况 3。
- 当 f (n) 与 n^log_b a 的大小关系介于情况 1 和情况 2 之间,或介于情况 2 和情况 3 之间时,主方法不适用。
4.6 证明主定理
4.6.1 对 b 的幂证明主定理
为了简化证明,先假设 n 是 b 的幂,即 n = b^k,其中 k 是整数。此时,n/b = b^{k-1},n/b² = b^{k-2},以此类推。
递归式展开: T(n) = aT(n/b) + f(n) = a(aT(n/b²) + f(n/b)) + f(n) = a²T(n/b²) + a f(n/b) + f(n) = ... = a^k T(1) + Σ_{i=0}^{k-1} a^i f(n/b^i)
其中,k = log_b n,a^k = a^{log_b n} = n^{log_b a}(由换底公式:a^{log_b n} = n^{log_b a})。
因此,T (n) = Θ(n^{log_b a}) + Σ_{i=0}^{k-1} a^i f (n/b^i)。
接下来,通过分析和式 Σ_{i=0}^{k-1} a^i f (n/b^i) 来证明三种情况:
- 情况 1:若 f (n) = O (n^log_b a - ε),则存在常数 c > 0 和 ε > 0,使得 f (n) ≤ c n^log_b a - ε。 代入和式得: Σ a^i f (n/b^i) ≤ c Σ a^i (n/b^i)^{log_b a - ε} = c n^{log_b a - ε} Σ a^i / (b^{i (log_b a - ε)}) = c n^{log_b a - ε} Σ (a / b^{log_b a - ε})^i = c n^{log_b a - ε} Σ (b^ε)^i (因为 a = b^{log_b a}) 这是一个公比为 b^ε > 1 的等比数列,和为 O (b^{ε k}) = O (n^ε)。 因此,Σ = O (n^{log_b a - ε}・n^ε) = O (n^{log_b a}),故 T (n) = Θ(n^{log_b a})。
- 情况 2:若 f (n) = Θ(n^log_b a log^k n),则: Σ a^i f (n/b^i) = Θ(Σ a^i (n/b^i)^{log_b a} log^k (n/b^i)) = Θ(n^{log_b a} Σ log^k (n/b^i)) 当 k=0 时,Σ log^0 (n/b^i) = Σ 1 = k = Θ(log n),故 Σ = Θ(n^{log_b a} log n)。 对于 k > 0,可通过归纳法证明 Σ = Θ(n^{log_b a} log^{k+1} n)。 因此,T (n) = Θ(n^{log_b a} log^{k+1} n)。
- 情况 3:若 f (n) = Ω(n^log_b a + ε) 且满足正则条件,则: 由正则条件 a f (n/b) ≤ c f (n),可得 a^i f (n/b^i) ≤ c^i f (n)。 因此,Σ a^i f (n/b^i) ≤ f (n) Σ c^i = O (f (n))(因为 c < 1,等比级数和有界)。 同时,Σ a^i f (n/b^i) ≥ f (n)(第一项),故 Σ = Θ(f (n))。 因此,T (n) = Θ(f (n))。
4.6.2 向下取整和向上取整
实际中,n 不一定是 b 的幂,此时 n/b 可能需要向下取整(⌊n/b⌋)或向上取整(⌈n/b⌉)。可以证明,这种取整操作不会改变递归式解的渐近阶。
例如,对于递归式 T (n) = a T (⌊n/b⌋) + f (n),可以证明:
- 存在常数 k,使得⌊n/b^i⌋ ≥ n/b^i - k。
- 通过适当调整常数,可证明其解与 n 是 b 的幂时的解具有相同的渐近阶。
因此,主定理对于 n 不是 b 的幂的情况同样成立。
思考题
- 最大子数组问题的变形:如何求解最大子数组问题的非递归版本(如 Kadane 算法)?其时间复杂度是多少?
- 递归式求解:使用代入法、递归树方法和主方法求解以下递归式:
- T(n) = 4T(n/2) + n
- T(n) = 4T(n/2) + n²
- T(n) = 4T(n/2) + n³
- Strassen 算法的优化:Strassen 算法的时间复杂度是 O (n^2.807),是否存在时间复杂度更低的矩阵乘法算法?目前的最优结果是什么?
- 分治策略的应用:除了本章介绍的问题,分治策略还可以应用于哪些问题?试举例说明其分治思路。
本章注记
- 分治策略是算法设计中的一种重要思想,其核心是将问题分解为更小的子问题,递归求解后合并结果。
- 最大子数组问题和 Strassen 矩阵乘法是分治策略的经典应用,分别将时间复杂度从 O (n²) 和 O (n³) 降低到了 O (n log n) 和 O (n^2.807)。
- 递归式的求解是分析分治算法复杂度的关键,代入法、递归树方法和主方法是三种常用的求解工具,其中主方法最为高效,但适用范围有限。
- 主定理的证明过程展示了递归式展开和求和的技巧,有助于深入理解分治算法的复杂度分析。

分治策略在排序算法(如归并排序、快速排序)、查找算法(如二分查找)、计算几何(如最近点对问题)等领域都有广泛应用,是每个程序员必须掌握的基本算法思想。

希望本文能帮助读者深入理解分治策略及其应用。文中的代码均经过测试,可以直接编译运行,读者可以动手实践,进一步体会分治策略的精髓。如有疑问或建议,欢迎在评论区留言讨论!
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2026-01-20,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

