算法基础学习笔记——⑦KMP\Trie\并查集
算法基础学习笔记——⑦KMP\Trie\并查集

命运之光
发布于 2024-03-20 10:55:41
发布于 2024-03-20 10:55:41
✨博主:命运之光 ✨专栏:算法基础学习

在这里插入图片描述
前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!
✨KMP
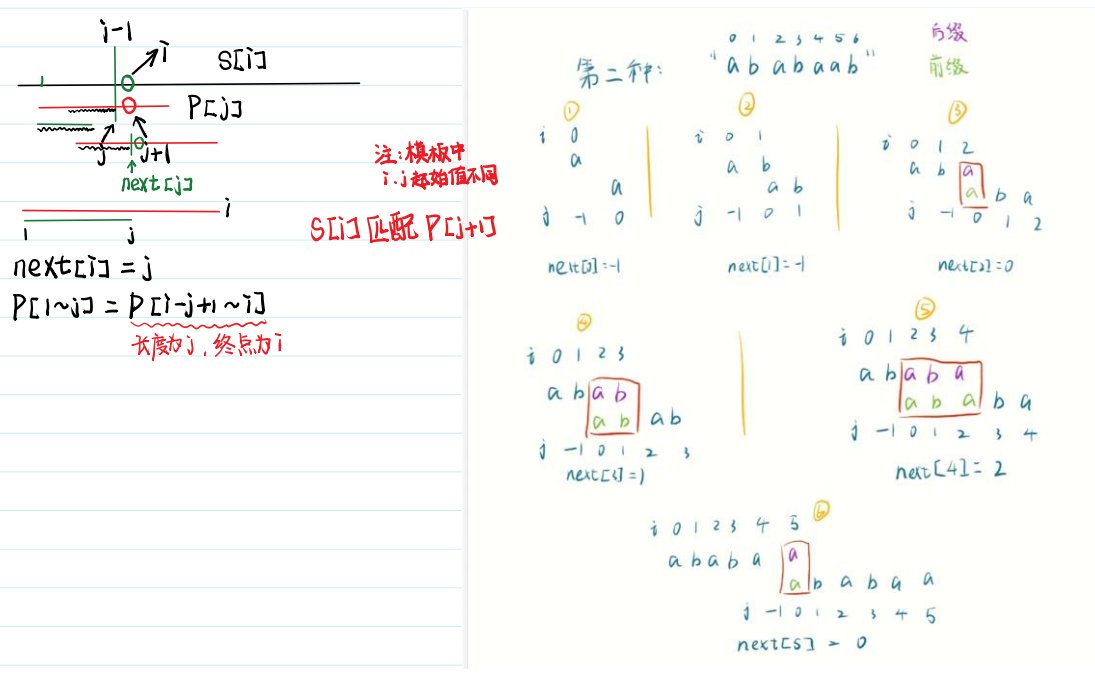
🍓KMP模板:
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
求模式串的Next数组:
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的逻辑
}
}✨Trie
Trie:高效的存储和查找字符串集合的数据结构
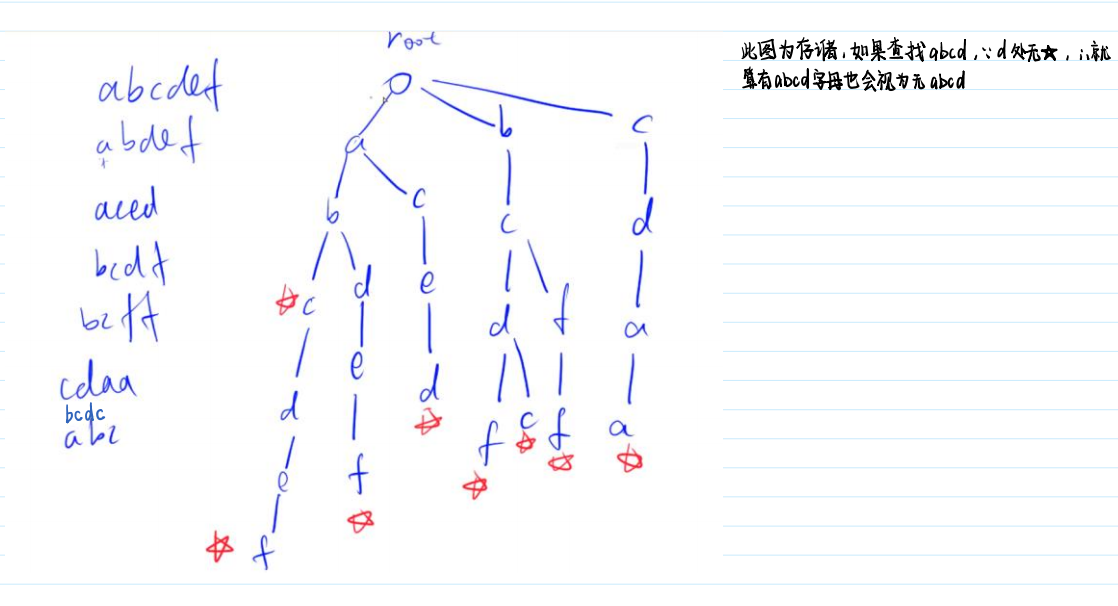
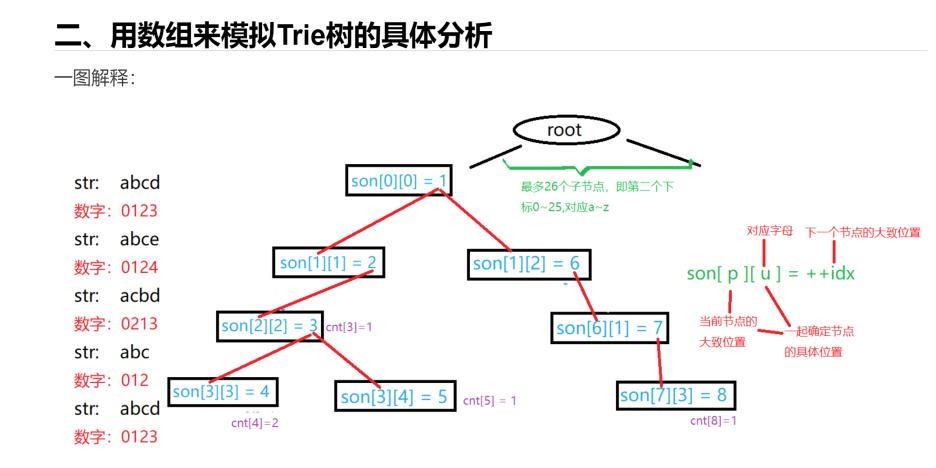
🍓Trie树模板:
//一般有26个字母 //idx存的是当前用到的下标
int son[N][26], cnt[N], idx;
// 0号点既是根节点,又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量
// 插入一个字符串
void insert(char *str)
{
int p = 0;//p为节点
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';//将a~z映射成0~25
if (!son[p][u]) son[p][u] = ++ idx;
p = son[p][u];
}
cnt[p] ++ ;//画 的点
}
// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
✨并查集
1.将两个集合合并
2.询问两个元素是否在一个集合当中
基本原理:每个集合用一颗树来表示。树根的编号就是整个集合的编号。
每个结点储存它的父节点,p[x]表示x的父节点
问题1:如何判断树根:if(p[x]==x)
问题2:如何求x的集合编号:while(p[x]!=x)x=p[x];
问题3:如何合并两个集合:px是x的集合编号,py是y的集合编号。p[x]=y
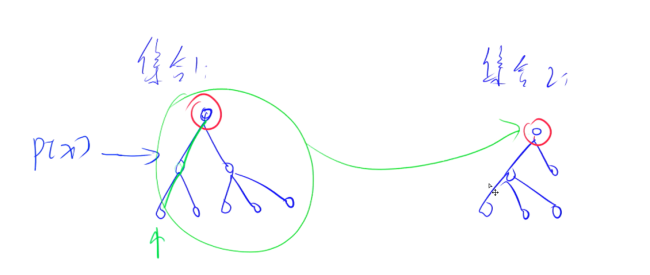
🍓并查集模板:
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2023-05-27,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

