从零开始深入理解奇异值分解（SVD）

SVD将一个复杂的矩阵变换分解为旋转-拉伸-旋转三个基本操作，提供了关于矩阵秩、四大子空间和最佳低秩近似的完整信息。其推导基于对称矩阵的特征分解，具有坚实的数学基础，可以说是线性代数中最重要、最优雅的分解之一，它提供了理解矩阵基本结构的一个强大框架。

1. 直观理解

先抛开数学公式，从几何角度来感受SVD，想象一个矩阵 A 作为一个线性变换，将一个空间中的向量（例如单位圆）映射到另一个空间（例如一个椭圆）。

SVD的核心思想是：任何矩阵的线性变换效果，都可以被分解为三个简单的基本变换：

• 一个旋转 (V*)：在原始空间（输入空间）中，找出一组标准的正交基（v₁, v₂, …, vₙ）旋转一下向量
• 一个缩放 (Σ)：在新的旋转后的坐标系下，对向量在各个坐标轴上进行纯粹的拉伸或压缩（缩放因子就是奇异值 σ₁, σ₂, …, σₙ），这是最关键的一步。
• 另一个旋转 (U)： 在缩放后的结果上，再进行一次旋转，将其放入目标空间（输出空间）中。

各变换解释： 假设一个 2x2 矩阵 A，对单位圆上所有的点进行变换，使得单位圆最终变成一个椭圆，SVD揭示了一个矩阵的“本质”的拉伸方向和强度，而撇开了旋转的影响。

• V* 的作用是：找到单位圆上的“主轴方向”（即椭圆的长轴和短轴方向在变换前对应的方向）。
• Σ 的作用是：将这两个主轴方向分别拉伸 σ₁ 和 σ₂ 倍，这就形成了椭圆的长轴和短轴长度。
• U 的作用是：将这个拉伸后的椭圆（其轴可能与坐标轴对齐）旋转到它在目标空间中的最终朝向。

2. 数学推导

数学定义 对于任意一个 m × n 的实数矩阵 A，其奇异值分解为：

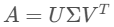
其中：

数学推导 SVD可以被看作是特征分解在任意矩阵上的推广，特征分解只适用于方阵，而SVD适用于任何矩阵。

2.1 构造对称方阵：

对于一个 m × n 的实数矩阵 A，其转置Aᵀ为一个n × m的实数矩阵，考虑 AᵀA 和 AAᵀ两个实对称方阵（并且是半正定的），其中

• AᵀA 是 n × n 的。
• AAᵀ 是 m × m 的。

2.2 特征分解：

根据实对称矩阵的性质，AᵀA 和 AAᵀ 都可以被正交对角化：

2.3 连接特征值与奇异值：

从下面的推导可以得出结论是：AᵀA 和 AAᵀ 拥有相同的非零特征值。 假设 λ 是 AᵀA 的一个特征值，v 是其对应的特征向量，那么：

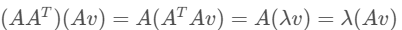
这说明 λ 也是 AAᵀ 的特征值，而其对应的特征向量是 A v（需要归一化）。

2.4 组装SVD：

从 AᵀA 的特征分解中得到 V 和奇异值 (Σ 的对角元素)。

左奇异向量 U 可以通过 ui=(1/σi)∗Avi 来计算（对于所有 σ_i > 0 的项），对于 σ_i = 0 的项，U 的剩余列可以任意扩充为一组标准正交基。

3. 原理分析与性质

降维与矩阵的真正秩 SVD特性之一是它可以可靠地确定矩阵的秩，数值计算中，由于浮点数精度问题，判断一个矩阵的秩是很困难的（某个特征值到底是0还是1e-15？）。

最佳低秩逼近 这是SVD的一个极其重要的应用。如果我们想用一个秩为 k（k < r）的矩阵 A_k 来近似原始矩阵 A，那么在弗罗贝尼乌斯范数（Frobenius norm）和谱范数（spectral norm）意义下的最佳近似是：

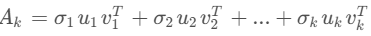
也就是说，我们只需保留前 k 个最大的奇异值及其对应的奇异向量，丢弃那些不重要的（小的）奇异值分量。这构成了数据压缩、降维和去噪的数学基础。

4. 示例

验证成功！

这个例子很简单，但展示了SVD的组成部分， 对于非对角矩阵，计算过程更复杂，但原理相同。

5. 应用场景

• 点云配准/ICP：求解两组点云之间的最佳刚体变换（旋转 R 和平移 t）。通过SVD可以优雅地求出使得对应点距离和最小的最优 R。
• SLAM中的矩阵分解：在解决优化问题时，例如求解线性系统 Ax=b，SVD可以提供数值稳定的解。
• 位姿估计：从本质矩阵或单应矩阵中恢复相机旋转 R 和平移 t 需要用到SVD。
• 矩阵伪逆 ：对于非方阵或奇异矩阵 A，其伪逆 A⁺ 可以通过SVD计算：A⁺ = V Σ⁺ Uᵀ，其中 Σ⁺ 是 Σ 的转置后非零元素取倒数。
• 降维与主成分分析 (PCA)：PCA本质上就是对数据的协方差矩阵进行特征分解（等同于对中心化后的数据矩阵进行SVD）。最大的奇异值对应的奇异向量就是最主要的主成分方向。