二叉树中迭代序遍历的空间复杂度是多少?
我一直在想,二叉树的迭代前置遍历(使用堆栈)的空间复杂度是多少。我参考了节目采访的内容,他们说
空间复杂度是O(h),其中h是树的高度,因为除了堆栈的顶部之外,堆栈中的节点对应于从根开始的路径上的节点的正确子节点。
以下是供参考的守则:
struct Node{
int data;
struct Node* left, right;
}
void printPreOrder(struct Node* root){
if(!root)
return ;
stack<struct Node* > s;
s.push(root);
while(!s.empty()){
struct Node *root_element = s.top();
cout<<root_element->data<<" ";
s.pop();
if(root_element->right){
s.push(root_element->right);
}
if(root_element->left){
s.push(root_element->left);
}
}
cout<<endl;
}
return ;
}我的直觉
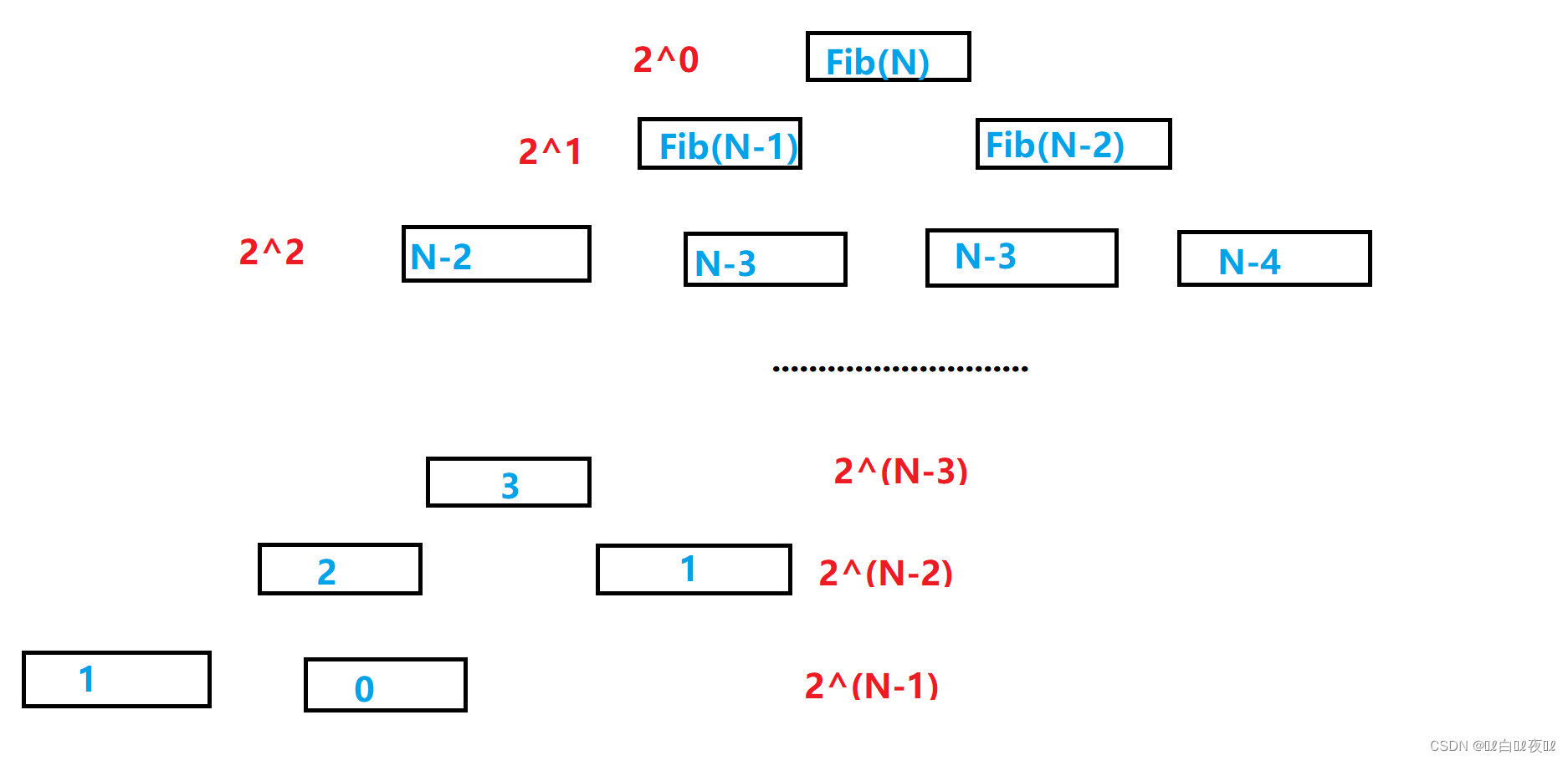
在研究该算法时,我观察到,在任何实例中,堆栈中的最大条目数可以是最大(num_of_leaves_in_left_subtree+1,num_of_trees_in_right_subtree)。由此可以推断,对于高度为h的树,最大叶数可为2^ h,因此,左子树中的最大树数为2^(h-1)。因此,堆栈中的最大条目数为2^(h-1)+1。因此,根据我的说法,上述算法的空间复杂度为O(2^(log(N)。
回答 2
Stack Overflow用户
发布于 2018-07-15 13:14:01
首先,您的preorder traversal迭代实现有一个错误--您应该推送一个右节点,然后再推一个左节点,反之亦然。
现在解释一下--在每次迭代中,您都要深入一个层次,并在堆栈中添加2个元素(如果它们存在的话),同时弹出一个节点(父节点)。这意味着,最多增加一个新的元素时,你去一个级别下降。一旦到达最左边的节点并弹出它,就会对堆栈-> O(h)中的顶部节点重复相同的过程。
例如,
1
/ \
2 5
/ \ / \
3 4 6 7步骤0:1被添加到堆栈-> O(1)中
步骤1:1删除,2和5被添加-> O(2)
步骤2:2删除,3和4被添加-> O(3)
步骤3:3删除-> O(2)
步骤4:4删除-> O(1)
步骤5:5删除,6和7被添加-> O(2)
步骤6:6删除-> O(1)
步骤7:7已删除-> O(0)
正如你所看到的,空间复杂性总是与树的高度成正比。
在最坏的情况下(如果树看起来像列表),空间复杂性是O(1) for --您的实现(正如@Islam Muhammad所指出的),因为在while循环的每一次迭代中,都会从堆栈中删除一项,并添加一项(只有1子项)。
Stack Overflow用户
发布于 2018-07-15 06:24:51
让我们按顺序遍历算法来找出它。
尝试观察根节点处的整个树所需的最大堆栈大小将等于添加了1的左侧子树所需的堆栈的最大大小。
但是怎么做?
如果您仔细观察,您会发现,当我们处理根节点时,我们将向堆栈中添加右节点和左节点,然后将堆栈的顶部,即左侧节点进行处理。
因此,如果递归地定义用于查找所需堆栈的最大大小的函数,则如下所示:
function maxStackSizeReq(struct Node* root){
if(!root)
return 0;
return maxStackSizeReq(node->left)+1;
}现在解释一下--在每次迭代中,您都要深入一个层次,并在堆栈中添加2个元素(如果它们存在的话),同时弹出一个节点(父节点)。这意味着,最多增加一个新的元素时,你去一个级别下降。一旦到达最左边的节点并弹出它,就会对堆栈-> O(h)中的顶部节点重复相同的过程。
例如,让我们尝试找出以下树所需的最大堆栈大小。
1
/ \
2 5
/ \ /
3 4 6 步骤0:调用maxStackSizeReq(root_1) ->返回maxStackSizeReq(root_2)+1这里的意思是,所需堆栈的最大大小将是左子树+1所需的堆栈大小。
2
/ \
3 4步骤2:调用maxStackSizeReq(root_2) - > return maxStackSizeReq(root_3)+1这里的意思是,所需堆栈的最大大小将是左子树+1. 3所需的堆栈大小。
步骤3:在这里调用maxStackSizeReq(root_3) - > return maxStackSizeReq(root_3->left which is NULL)+1我们的意思是,所需堆栈的最大大小将是左子树所需的堆栈大小,即NULL + 1。
因此,步骤3返回1 -> 步骤2返回2 -> 步骤1返回3;
最后,函数将返回3作为处理根节点树的预顺序遍历所需的最大堆栈大小。
时间复杂度O(h)如何?,如果你仔细遵循上面的算法,你也会发现我们只遍历树的左子树。因此,当执行O(h)递归调用时,上述算法的空间复杂度为O(h)。最后,预序迭代堆栈实现的空间复杂度也将是O(h)。
记住
有时,您可能会听到预序或无序迭代解的空间复杂性是O(n)。但是,请记住,O(h)是一个更好的答案,因为空间复杂度仅为O(n),当h变为n时,这是相当明显的。
1
\
2
\
3https://stackoverflow.com/questions/51347487
复制相似问题

![[数据结构] 二叉树的前序遍历、中序遍历和后序遍历](https://ask.qcloudimg.com/http-save/yehe-6872954/dswy4new2c.png)