两个矩阵中相似特征谱的匹配
我有两个矩阵，其中一个矩阵的特征谱部分非常类似于另一个矩阵的特征谱，但我(目前)唯一能够证实这一点的方法是非常不雅观的。
我对任何解决方案都是开放的，但在这里我发现使用MATLAB语法是最容易的:在第一个例子中，我将定义矩阵A和B，这样B的两个特征值也可以在A中找到，而B的对应的两个特征向量也是具有相同特征值的A的特征向量，但如果不使用与A共享特征值的B的特征向量，并“搜索”这些特征向量是否在A中具有相同的特征值，这一点就不明显了。
下面是两个这样的矩阵的示例：A和B
A = diag([1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1]);
B = diag([19.9385 7.6177 17.2969 9.6177 11.3208 -1 8.6792 1 11.3208 -1 8.6792 1 19.9385 7.6177 17.2969 9.6177]);
B(2,1) = 9.2832; B(4,3)=B(2,1); B(14,13)=-B(2,1); B(16,15)=-B(2,1);
B = tril(B,-1)'+B; % Make it Hermitian by mirroring the lower triangle into the upper triangle通过运行命令[eig(A)' ; eig(B)']，我们可以看到A的两个特征值(都是-1)与B的特征值共享(上行是A，下行是B )：
-1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 1 1 1
-1 -1 1 1 8 8 9 9 10 10 11 11 17 17 20 20A的特征向量-1也将B的特征向量与-1的特征值相匹配，但当它们出现在A的特征向量矩阵VA的第1和第2列时，它们出现在B的特征向量矩阵VB的第4和第6列中。
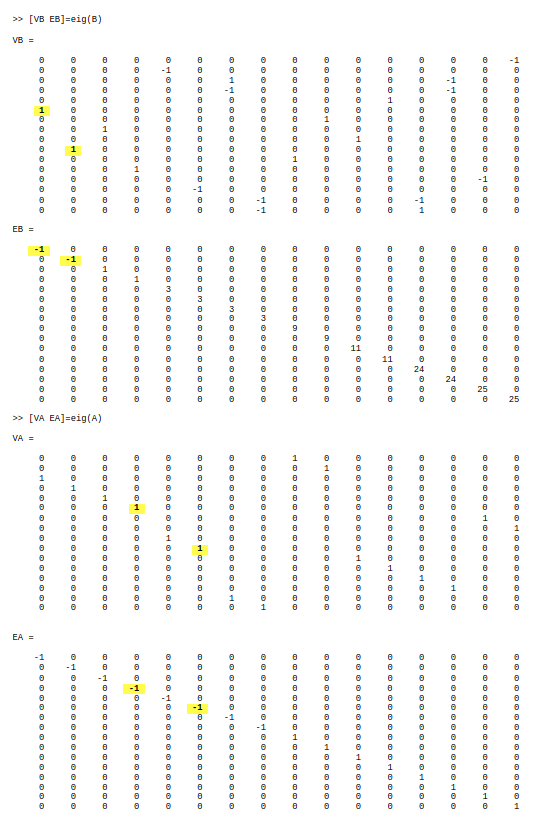
是否有一种更优雅的方法来查看这一点，而不需要蛮力搜索来查看公共特征值的特征向量是否是共享的？
这里有一个稍微复杂一些的例子，其中矩阵大小不一样，特征向量不再是完全相同的，但它们仍然是等价的(具有相同特征值的特征向量)：
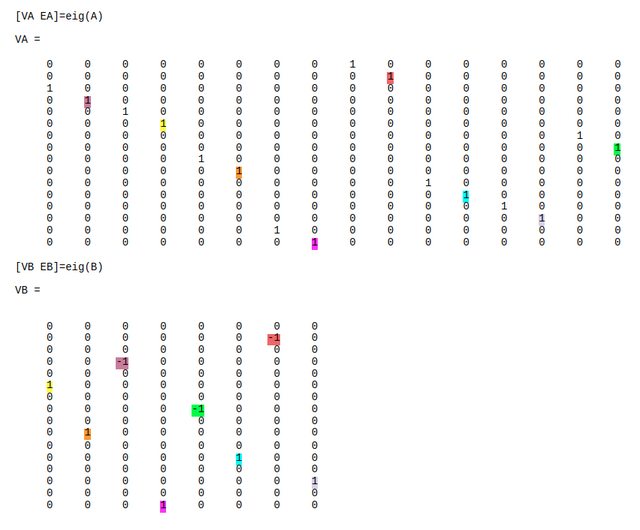
我已经搜索了相当多的解决方案，并且可以说我知道一些相关的工具，例如：
- 命令，但不幸的是，这不能用于对上述特征向量进行排序。
- 两个矩阵的同时对角化，听起来很相关，但似乎对这个目标没有帮助。
- 在Mathematics.SE上提出了另一个“同时对角化”问题，但没有收到任何答复(尽管这是一个用于提取与注释
k的特征值相对应的特征向量的有用命令：V(:,diag(D)==k))。 - 矩阵必须通勤才能共享特征向量。，但这只是告诉我，当两者都试图匹配特征向量，并没有使我更接近我的目标，能够优雅地匹配特征向量。
回答 1
Stack Overflow用户
发布于 2021-11-13 22:43:51
我将首先比较所有的特征值和所有的特征向量，然后看看特征值和特征向量是否同时匹配。
我不知道这种方法是否更优雅。这可能是更野蛮的力量。但是，您可以摆脱繁琐的搜索和匹配特征值-特征向量过程，这段代码应该更短。
特征向量是通过取内积来比较的，因为它们比外部积更容易实现。由于matlab对特征向量进行了自动归一化，利用柯西-施瓦兹不等式，线性相关特征向量的内积应该是-1或1。
% compare eigenvalues
is_val_same = abs(diag(EA)-diag(EB).') < 1e-8;
% total number of eigenvectors
m=size(VA,2);
n=size(VB,2);
% calculate dot products
dotAB = sum(permute(repmat(conj(VB), 1, 1, m), [1 3 2]).*repmat(VA, 1, 1, n), 1);
dotAB = reshape(dotAB, m, n);
% compare eigenvectors
is_vec_same = abs(abs(dotAB)-1) < 1e-8;
% find the matching eigen pairs
[index_A, index_B]=find(is_vec_same & is_val_same)输出：
index_A =
4
6
16
12
index_B =
1
2
3
4这意味着4 6 16 12 of A分别对应于B的1 2 3 4列。
当矩阵大小不相同时，它也能工作。可以通过寻找A和B的重复特征向量来识别Dengeneracy，使用与上面类似的代码。
https://stackoverflow.com/questions/65986534
复制
相似问题
用jaccard系数构造相似矩阵的谱聚类
相似矩阵->特征向量算法？
OpenCV特征匹配图像中的多个相似对象
特征向量(谱)分解
质谱数据的特征选择
领取专属 10元无门槛券
AI混元助手 在线答疑
洞察 腾讯核心技术
剖析业界实践案例
腾讯云开发者
