凸优化整理(四)
对偶理论
考虑如下一般形式约束优化问题:

记可行集为
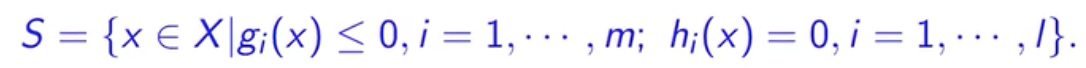
这里跟之前不同的地方在于x∈X。之前我们都在说的是连续性问题,即X=(R^n);在对偶理论中包含了离散性的问题,X可能是整数集合,即X=(Z^n),或者正整数集合X=(Z^n+),或者0-1规划,即X=({{0,1}}^n),也可以任何自定义的集合,如X={x| (e^Tx=1),x≥0};(P)在对偶理论中称为原问题(primal problem)。
- 如果问题(P)非凸,它是一个NP难的问题。此时我们可以寻找一个与(P)紧密,简单的对偶问题(D)。
- 线性规划的原问题(P),min (c^Tx),s.t. Ax=b,x≥0。虽然可以使用单纯形法和内点法来求解,但依然可以使用其对偶问题(D)max (b^Ty),s.t. (A^Ty≤c)来求解。
- 鲁棒优化,锥优化跟对偶问题在某些前提下具有一定的等价关系。
- 拉格朗日对偶函数
引进拉格朗日函数:
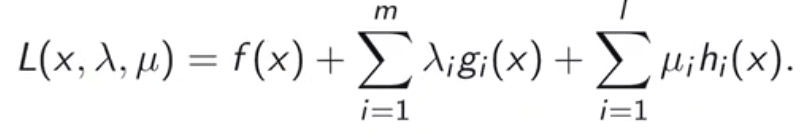
拉格朗日对偶函数(简称对偶函数):
d(λ,μ) = (min_{x∈X}){f(x)+(\sum_{i=1}^mλ_ig_i(x))+(\sum_{i=1}^lμ_ih_i(x))}
∀(λ,μ),λ≥0 ≤ (min_{x∈S}){f(x)+(\sum_{i=1}^mλ_ig_i(x))+(\sum_{i=1}^lμ_ih_i(x))}
≤ (min_{x∈S}){f(x)}
即∀(λ,μ),λ≥0,必有d(λ,μ)≤v(P)(P问题的最优值),即d(λ,μ)是v(P)的下界。由不同的(λ,μ)可以产生不同的下界,下界越大越好,可以更加容易接近于x的最小值。
- 拉格朗日对偶问题
简称对偶问题
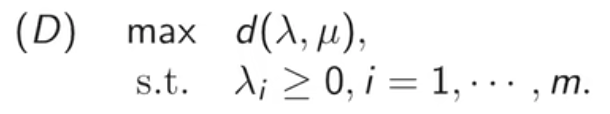
即在许多个λ中找一个最大的d(λ,μ),整体而言就是拉格朗日函数
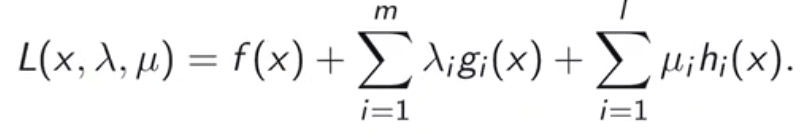
(D) (max_{λ≥0,μ} min_{x∈X}L(x,λ,μ)),先对拉格朗日函数中的x求一个最小,再对(λ,μ)求最大。
现在我们将D问题交换一下位置
(min_{x∈X} max_{λ≥0,μ}L(x,λ,μ)),先对拉格朗日函数中的(λ,μ)求最大,再对x求最小。我们先来看一下对拉格朗日函数中的(λ,μ)求最大
(max_{λ≥0,μ}) {f(x)+(\sum_{i=1}^mλ_ig_i(x))+(\sum_{i=1}^lμ_ih_i(x))}
当(g_i(x))≤0,(h_i(x))=0时,该问题最大就是f(x);否则就是+∞
- f(x) (g_i(x))≤0,(h_i(x))=0
- +∞ otherwise
+∞的情况直接忽略,只保留f(x),再加上外层的对x求最小,就是
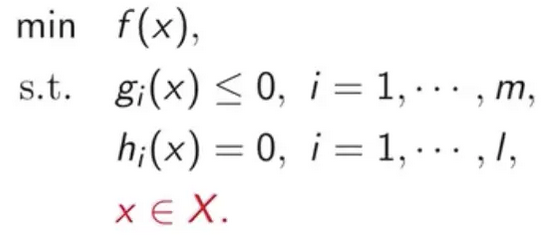
由此可知(min_{x∈X} max_{λ≥0,μ}L(x,λ,μ))其实就是原问题(P)
则原问题和对偶问题可以看成是对(λ,μ)求最大和x求最小先后顺序的交换,对L(x,λ,μ)函数两种不同的处理方式得到了原问题P和对偶问题D。
- 几何解释
(P) min f(x)
s.t. g(x)≤0
x∈X
由以上原问题可知拉格朗日函数以及对偶函数为
L(x,λ)=f(x)+λg(x)
d(λ)=(min_{x∈X}){f(x)+λg(x)}
则对偶问题为
(D) (max_{λ≥0}) d(λ)
我们把f(x),g(x)转换一下
G={(y,z)| g(x)=y,f(x)=z,x∈X}
那么原问题可以转换为
(P) min z s.t. y≤0,(y,z)∈G
对偶问题转换为
(D) (max_{λ≥0}) d(λ)
where d(λ)=(min_{(y,z)∈G}){z+λy}
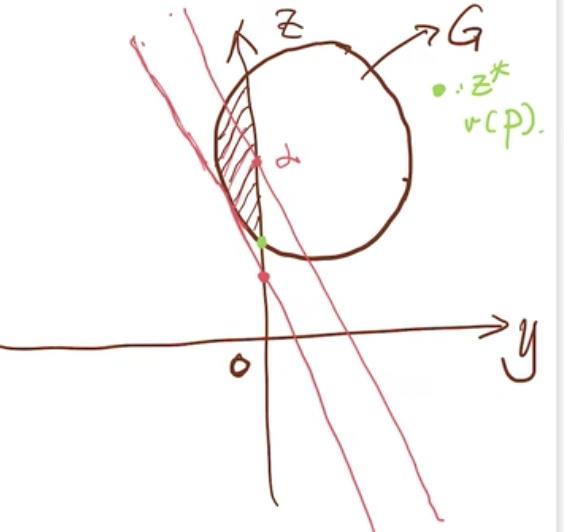
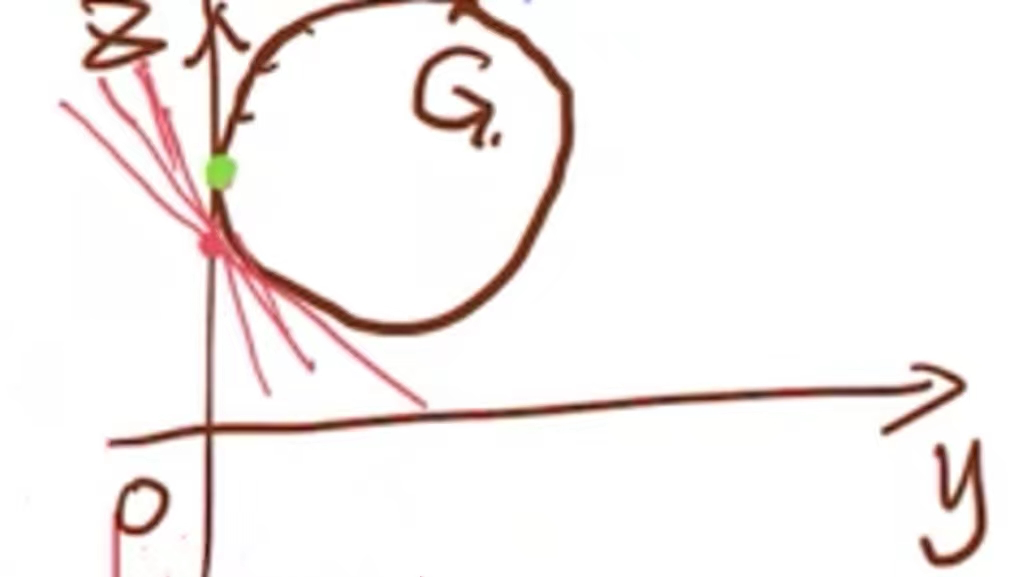
在上图中横轴是y轴,纵轴是z轴,圆圈范围内为G集合。原问题P中,y≤0对应G中就是阴影中的范围,求z最小,就是z轴上绿点的位置,它是G这个圆的下端与z轴相交的位置。在对偶问题D中,我们令z+λy=α,则z=-λy+α,我们把λ看成一个给定的值,且λ≥0,α看成一个常数,则z=-λy+α就是一个斜率为非正,截距为α的直线,我们假设这条直线就是上图中上端的直线。在D问题中的 d(λ)=(min_{(y,z)∈G}){z+λy}其实就是在找截距α最小,那么在上图中最小的截距就是下端这个与G相切的直线的截距最小(因为再向下移动,就不在G的范围内了),那么该直线与z轴的交点就是d(λ)。
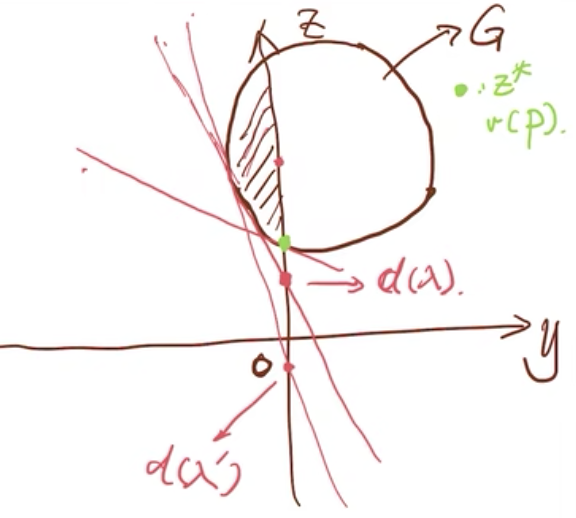
在D问题中, (max_{λ≥0}) d(λ)就是要找出一个最大的截距,此时我们需要调整-λ(斜率)来使得直线即要与阴影部分的圆相切,又要保证斜率为非正的,那么此时与绿点相切的直线就是最大的d(λ)。由此,我们可以看到原问题P和对偶问题D都汇集到了一个点上,即v(P)=v(D)。
但并不是所有情况都有v(P)=v(D),如下图所示
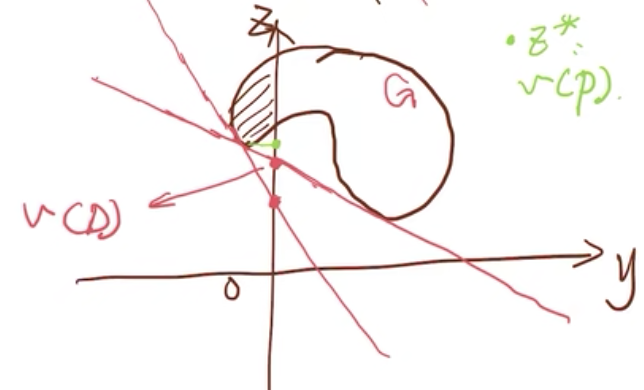
在上图的情况时,v(D)<v(P),所以说d(λ)≤v(P),为v(P)的下界。原问题P是在可行集的内部(阴影部分)找一个点,使得这个点的位置尽可能的要靠下(z轴尽可能的小);对偶问题D是找出很多与G相切的面,这些面都会跟z轴有交点,我们希望找到一个跟z轴交点最大的切平面。
- 写出线性规划的对偶问题
给出如下线性规划问题的对偶问题:
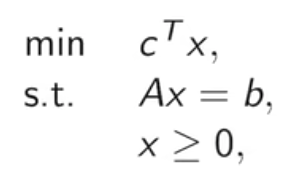
其中
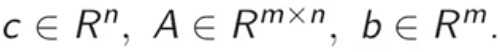
这个问题我们既可以把x≥0看成是x∈X,则这里没有不等式约束,也可以把x≥0看成是-x≤0的等式约束都可以。这里我们采用第一种方式。
拉格朗日函数就为L(x,μ)=(c^Tx)+(μ^T)(b-Ax)
对偶函数为d(μ)=(min_{x≥0}){ (c^Tx)+(μ^T)b-(μ^T)Ax}
=(min_{x≥0}){((c-A^Tμ)^Tx+b^Tμ)}
因为x≥0的,上式要求最小,只有两种情况
- (b^Tμ) if c-(A^Tμ)≥0
- -∞ otherwise
在对偶问题D中
max d(μ)
由于d(μ)已经求出,-∞对我们没有任何帮助,直接剔除,则最终对偶问题为
max (b^Tμ)
s.t. (A^Tμ)≤c
- 弱对偶定理
设v(P)是原问题(P)的最优值,v(D)是对偶问题(D)的最优值,则v(D)≤v(P)。
任取x∈S,(λ,μ),λ≥0,必有d(λ,μ)≤f(x)
d(λ,μ)≤v(D)≤v(P)≤f(x)
推论:假设
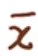
∈S,(

,
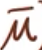
),

≥0,且d(

,
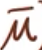
)=f(
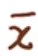
),则v(P)=v(D),且
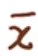
,(

,
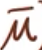
)是(P)和(D)的最优解。
d(

,
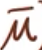
)=v(D)=v(P)=f(
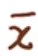
)
推论:若v(P)=-∞,则d(λ,μ)=-∞,∀(λ,μ),λ≥0;
若v(D)=+∞,则(P)无可行解。
Duality gap:v(P)-v(D)>0
考虑下列约束优化问题

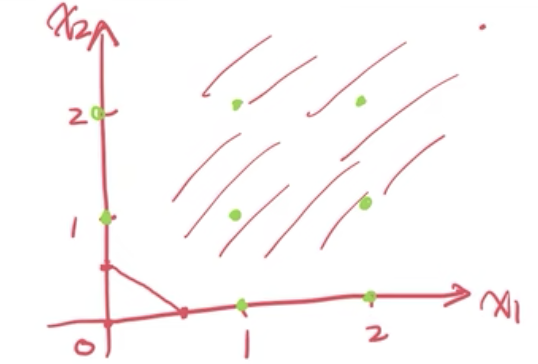
在上图中,以((1\over 2),(1\over 2))线段为边界向外扩展的阴影部分为可行区域,同时x要求为正整数,则图中绿色的点才是满足要求的部分。目标函数是一个以原点为中心不断向外扩展的圆,那么这个圆能接触到的第一个可行点(绿色的点)即为最小值。那么该圆能接触到的第一个点要么是(1,0)要么是(0,1),则
v(P)=1
现在我们来看一下对偶问题的最优值
对偶函数为d(λ)=(min_{x∈Z_+^2}){(x_1^2+x_2^2)+λ((1\over 2)-(x_1-x_2))}
=(min_{x∈Z_+^2}){((x_1-{λ\over 2})^2+(x_2-{λ\over 2})^2+{λ\over 2}-{λ^2\over 2})}
从上式可以看出,(x_1)和(x_2)没有交叉项,只需要分别求最小即可。则我们只需要关心
(min_{x∈Z_+^2})((x-{λ\over 2})^2)
我们只需要看哪个整数点离对称轴(λ\over 2)近即可,那么我们需要知道(λ\over 2)到底是什么情况
当0≤(λ\over 2)≤(1\over 2),即0≤λ≤1时,必然是0离(λ\over 2)近,代入d(λ),此时最小值为(λ\over 2);
当(1\over 2)≤(λ\over 2)≤(3\over 2),即1≤λ≤3时,必然是1离 (λ\over 2)近,代入d(λ),此时最小值为2-(3\over 2)λ;
当(3\over 2)≤(λ\over 2)≤(5\over 2),即3≤λ≤5时,必然是2离(λ\over 2)近,代入d(λ),此时最小值为8-(7\over 2)λ;
......
即为
- (λ\over 2) if 0≤λ≤1
- 2-(3\over 2)λ if 1≤λ≤3
- 8-(7\over 2)λ if 3≤λ≤5
- .......
由此可见,d(λ)是一个分段线性函数,它们有不同的斜率,从第2个分段开始,它们的斜率都是负的,画出函数图形如下
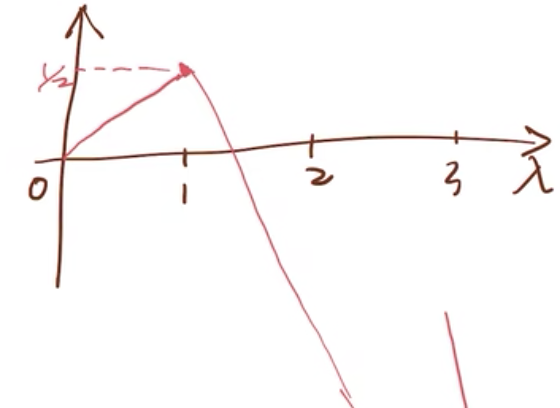
对偶问题(D)为
max d(λ)
s.t. λ≥0
由上图可知,最大值为(1\over 2)
对于这个整数规划,gap=v(P)-v(D)=1-(1\over 2)=(1\over 2)
- 强对偶定理
假设:
- 集合X为非空凸集,f(x)及(g_i)(x),i=1,...,m是凸函数,(h_i)(x),i=1,...,l均为线性函数;即原问题P是一个凸优化问题。
- 假设存在

∈X使得

(严格可行点),且0∈int h(X),其中h(X)={((h_1(x),...,h_l(x))^T|x∈X)}(0是h(X)集合的内点),则强对偶成立(v(P)=v(D)),即
在对偶问题的几何解释中有这样两个图形


的严格可行点((g_i)(

)<0)指的是在G集合中位于z轴左边的部分,不包含z轴,这里无论G集合是否是凸集。如果

不是一个严格可行点,那么就意味着G集合位于z轴的右边,或者与z轴有相交的部分。
在上图中,G与z轴相切,虽然我们可以找到一个原问题P的解(图中绿色的点),但是对于对偶问题D来说,斜率(-λ),当λ越大,这条直线就会越陡峭,直到λ->∞的时候,直线与z轴重合,D的解才可能达到绿点。对于这种情况,我们一般是排除的,所以才有了严格可行点。
证明:由于

的存在,(P)有可行点
若v(P)=-∞,则d(λ,μ)=-∞,∀(λ,μ),λ≥0
若v(P)=γ,γ是一个有界值,则不存在x∈X,使得f(x)<γ,(g_i(x))≤0,i=1,...,m,(h_i(x))=0,i=1,...,l
定义H={((p,q,r)^T)∈(R^{1+m+l})| f(x)-γ<p,(g_i(x))≤(q_i),i=1,...,m,(h_i(x))=(r_i),i=1,...,l,x∈X}
由f(x)是凸函数,(g_i(x))是凸函数,X是凸集合,可知H是凸集合,且((0,0,0)^T)∉H,这里第一个0是1维,第二个0是m维,第三个0是l维
根据凸集分离定理(见凸优化整理 中的支撑超平面定理),则存在((λ_0,λ,μ)^T)≠0,这里(λ_0)是1维,λ是m维,μ是l维,使得
((λ_0),λ,μ)((p,q,r)^T)≥((λ_0),λ,μ)((0,0,0)^T) ∀((p,q,r)^T)∈c|H(闭包)
即 ((λ_0),λ,μ)((p,q,r)^T)≥0,可得
(λ_0p)+(λ^Tq)+(μ^Tr)≥0, ∀((p,q,r)^T)∈c|H (*)
则 (λ_0)≥0,(λ_i)≥0,i=1,...,m
由(*)可得,∀x∈X,(λ_0)(f(x)-γ)+(\sum_{i=1}^mλ_ig_i(x))+(\sum_{i=1}^lμ_ih_i(x))≥0 (#)
不妨设(λ_0)=0
(#)即 (\sum_{i=1}^mλ_ig_i(x))+(\sum_{i=1}^lμ_ih_i(x))≥0,∀x∈X
可将

代入上式得
(\sum_{i=1}^mλ_ig_i)(

)+(\sum_{i=1}^lμ_ih_i)(

)≥0
由于(g_i)(

)<0,(h_i)(

)=0,必有(λ_i)=0,i=1,...,m
(#)即 (\sum_{i=1}^lμ_ih_i(x))≥0,∀x∈X (@)
由于 0∈int h(X),h(X)={((h_1(x),...,h_l(x))^T|x∈X)}
可知∃
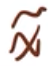
∈X,使得
(()(h_1)(
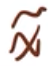
),...,(h_l)(
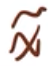
)()^T)=ɛ((-μ_1,...,-μ_l)^T)
将
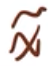
代入(@)可得
-ɛ(\sum_{i=1}^lμ_i^2)≥0,则只有(μ_i)=0,意味着((λ_0,λ,μ)^T)=0与 ((λ_0,λ,μ)^T)≠0矛盾,则必有
(λ_0)≠0,则意味着(λ_0)>0,(#)两边同除以(λ_0),令(λ_i\over λ_0)=
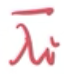
≥0,(μ_i\over λ_0)=

,得
f(x)-γ+(\sum_{i=1}^m)
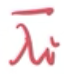
(g_i(x))+(\sum_{i=1}^l)

(h_i(x))≥0,∀x∈X
可得f(x) +(\sum_{i=1}^m)
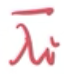
(g_i(x))+(\sum_{i=1}^l)

(h_i(x))≥γ,∀x∈X
可得d(

,
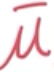
)≥γ=v(P)
故v(D)=d(

,
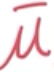
)=v(P) 得证
- 凸优化问题
一、f(x)及(g_i(x)),i=1,...,m是凸函数,(h_i(x)),i=1,...,l均为线性函数,X凸集;
二、若(x^*)满足KKT条件,则(x^*)是原问题(P)最优解,且乘子为对偶问题(D)的最优解。
(x^*)是KKT点,存在

,
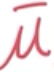
使得
- ∇f((x^*))+(\sum_{i=1}^m)
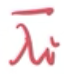
∇(g_i(x^*))+(\sum_{i=1}^l)

∇(h_i(x^*))=0
-
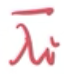
≥0
- (g_i(x^*))≤0,i=1,...,m
- (h_i(x^*))=0,i=1,...,l
-
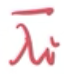
(g_i(x^*))=0,i=1,...,m
由1可知,(x^*)是拉格朗日函数 f((x^*))+(\sum_{i=1}^m)
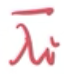
(g_i(x^*))+(\sum_{i=1}^l)

(h_i(x^*)) 的最小点(凸函数梯度为0的点必然是最小点)
对偶函数d(

,
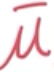
)= f((x^*))+(\sum_{i=1}^m)
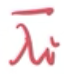
(g_i(x^*))+(\sum_{i=1}^l)

(h_i(x^*))= f((x^*))
故(

,
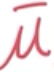
)是对偶问题(D)的最优解,且v(P)=v(D)
三、若Slater条件成立,则原问题(P)的最优解也是KKT点,相应乘子为对偶问题(D)的最优解。
- 鞍点与强对偶
(Ⅰ) 原问题(P)有最优解

,对偶问题(D)有最优解(

,
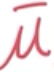
),满足强对偶v(P)=v(D)。
由以上我们可以知道的信息是
- (g_i)(

)≤0,
- (h_i)(

)=0,
-

∈X,
-

≥0,
- f(

)=d(

,
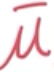
)
对偶函数d(

,
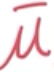
)=(min_{x∈X}){f(x)+(\sum_{i=1}^m)
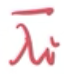
(g_i(x))+(\sum_{i=1}^l)

(h_i(x))}
= f(

)+(\sum_{i=1}^m)
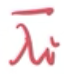
(g_i)(

)+(\sum_{i=1}^l)

(h_i)(

) (1)
= f(

) (2)
由等式(1)即 L(

,

,
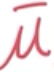
)=(min_{x∈X})L(x,

,
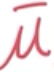
)
即 L(

,

,
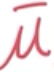
)≤L(x,

,
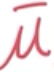
) ∀x∈X
由 L(

,λ,μ)=f(

)+(\sum_{i=1}^m)(λ_ig_i)(

)+(\sum_{i=1}^l)(μ_ih_i)(

) ∀λ≥0
由等式(2) ≤f(

)+(\sum_{i=1}^m)
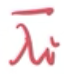
(g_i)(

)+(\sum_{i=1}^l)

(h_i)(

)
=L(

,

,
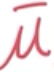
)
即 L(

,λ,μ)≤L(

,

,
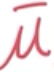
) ∀λ≥0
由以上综合可得
(Ⅱ) L(

,λ,μ)≤L(

,

,
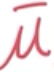
)≤L(x,

,
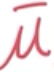
) ∀x∈X,λ≥0,μ
称(

,

,
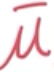
)是L(x,λ,μ)的鞍点,它意味着

是原问题(P)的最优解,(

,
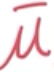
)是对偶问题(D)的最优解,并且强对偶成立。
这里(Ⅰ)和(Ⅱ)是等价的关系。
- 对偶问题的基本性质
这里我们不看原问题(P),只单独看对偶问题(D)
对偶问题:
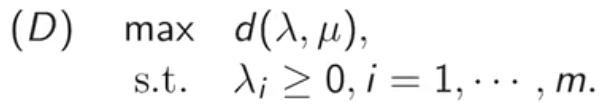
其中
d(λ,μ)=(min_{x∈X}){f(x)+(λ^T)g(x)+(μ^T)h(x)}
这里为了方便起见,记
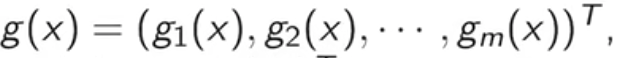
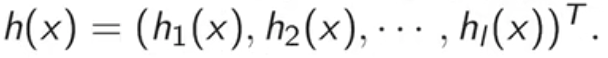
也就是说g(x)和h(x)是两个向量。
对偶问题(D)一定是凸问题,对偶函数是凹函数。
假设X有有限个点(x^1,x^2,...,x^N),则
d(λ,μ)=(min_{i=1...N}){f((x^i))+(λ^T)g((x^i))+(μ^T)h((x^i))}
f((x^i))+(λ^T)g((x^i))+(μ^T)h((x^i))是一个关于λ,μ的线性函数,线性函数既是凸函数也是凹函数。
我们这里设N=5

那么这里就是5条直线,以第4条直线为例,就是f((x^4))+(λ^T)g((x^4))+(μ^T)h((x^4)),其中 f((x^4))是常数项,g((x^4))是λ的线性项系数,h((x^4))是μ的线性项系数。
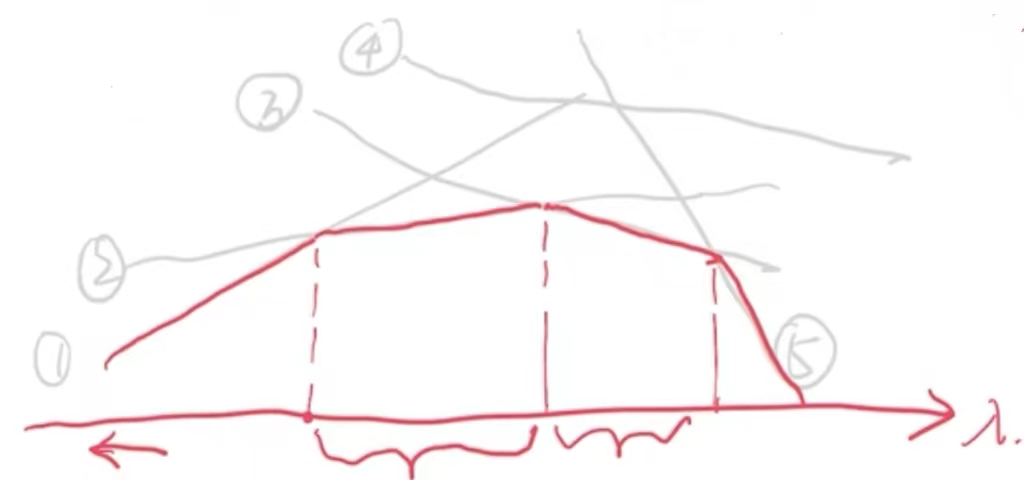
对这5条线性函数求最小,由于是一个二维图形,这里就只以λ的一元函数来说明(二元函数是一个三维的曲面,跟这里意思是一样),上图中红色线段的部分就是所有线性函数中最小的部分,它是一个开口向下的分片线性函数,是一个凹函数。
上面讨论的是X是有限个点,但如果X=(R_+^n),(Z_+^n)这样的无限集合,它依然是一个凹函数,只不过分片的连接点之间会更加的光滑而已。
- 割平面法(outting place method)
- (D) max d(λ,μ)
- s.t. λ≥0
<=>(等价)
- max θ
- s.t. θ=d(λ,μ)
- λ≥0
<=>
- max θ
- s.t. θ≤d(λ,μ)
- λ≥0
<=>
- max θ
- s.t. θ≤ (min_{x∈X}){f(x)+(λ^T)g(x)+(μ^T)h(x)}
- λ≥0
<=>
- max θ
- s.t. θ≤ f(x)+(λ^T)g(x)+(μ^T)h(x),∀x∈X (*)
- λ≥0
以上都是等价的,我们记最后这组等价式的最优解
,
=v(D)
假设X有有限个点(x^1,x^2,...,x^N),(*)即
θ≤ f((x^i))+(λ^T)g((x^i))+(μ^T)h((x^i)),i=1,...,N
那么上式就是有限个线性不等式,代入最后一组等价式中,总体它是一个线性规划的问题(LP),这样的问题终归是可以求解出来的(比方说使用专门的软件求解),对偶问题(D)就解决了。
如果N非常大,此时我们无法将这有限个不等式全部写出来;又或者X有无穷个点,(*)代表的是无穷多个线性不等式。此时这两种情况我们都无法使用软件工具去求解。
我们现在依然设N=5
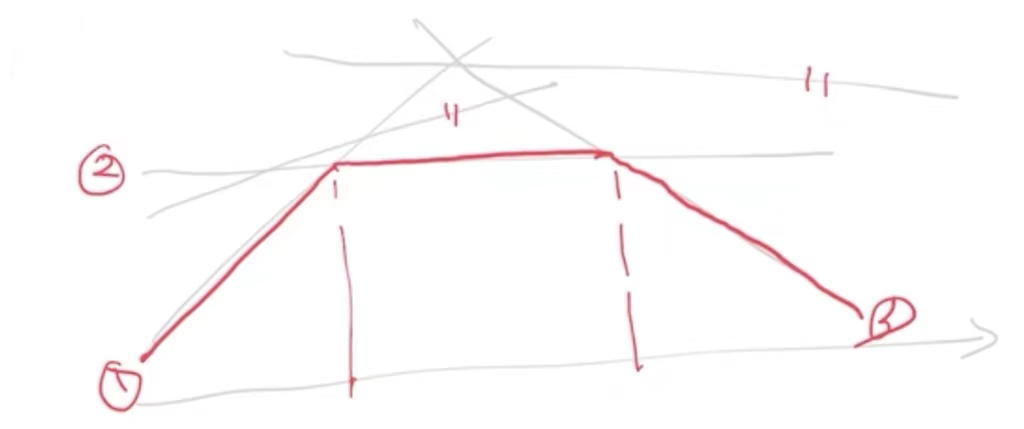
上图中,红色的线段部分就是D的图形,虽然上图中有5条线,但其实只有3条线起作用。如果X有无穷多个点,即有无穷多条线,那么真正起作用的线并不会有那么多的,那么我们只需要将起作用的线挑出来,不断地去试,这样的方法叫做割平面法。
现在我们任取X的子集(X^0),其中有两个点,比如(X^0)={(x^1,x^3)}。一开始我们并不知道真正起作用的是哪些点,所以这里的(X^0)是任取的。这样我们将等价式进行替换
- max θ
- s.t. θ≤ f(x)+(λ^T)g(x)+(μ^T)h(x),∀x∈(X^0)
- λ≥0
再向上的等价式替换
- max θ
- s.t. θ≤ (min_{x∈X^0}){f(x)+(λ^T)g(x)+(μ^T)h(x)}
- λ≥0
我们会发现这是对两个线性函数求最小,即对上图中的1,3两条直线的最小部分
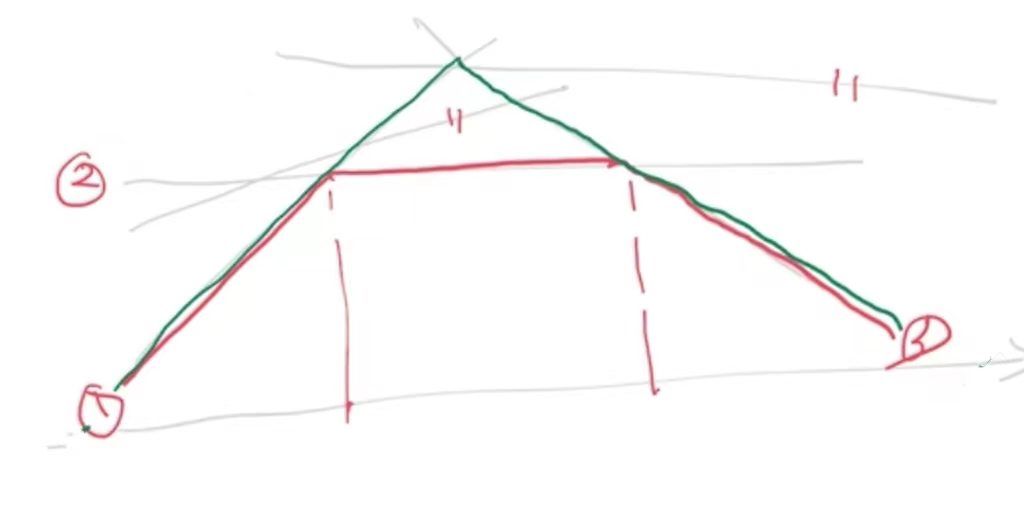
那么即是上图中绿色线段的部分。由于 θ≤ (min_{x∈X^0}){f(x)+(λ^T)g(x)+(μ^T)h(x)},也就是说θ是包含了这两条绿线下方的所有部分,而max θ即是这两条绿线,此时
θ= (min_{x∈X^0}){f(x)+(λ^T)g(x)+(μ^T)h(x)}
绿色的这一段是原来的函数d(λ,μ)(红色线段部分)的一个近似函数。我们记这个近似函数为(θ^0),记原函数为

,近似函数是从原函数的上方进行近似的,所以 (θ^0)≥

。
我们记这个等价式替换的最优解为((λ^0),(μ^0),(θ^0)),计算d( ((λ^0),(μ^0)),即求解
(min_{x∈X}){f(x)+((λ^0)^T)g(x)+((μ^0)^T)h(x)}得到最优解(x^0)
判断:1)若(x^0)满足g((x^0))≤0,h((x^0))=0,((λ^0)^T)g((x^0))=0,则
f((x^0))=f((x^0))+ ((λ^0)^T)g((x^0))+((μ^0)^T)h((x^0))
= d((λ^0),(μ^0))
这意味着强对偶成立,(x^0)是(P)的最优解,((λ^0),(μ^0))是(D)的最优解。这相当于一步到位,我们通过两个点就找到了最优解,这种情况是不太可能的。
2)若d((λ^0),(μ^0))=(θ^0),则

=v(D)≤(θ^0)=d((λ^0),(μ^0)),由于v(D)是对偶问题(D)的最大值,则它不可能小于(θ^0),故只能是v(D)=(θ^0),即 d((λ^0),(μ^0))=v(D),此时我们已经求出了(D)的最优解。
如果以上这两种情况都没有发生,说明选择的(x^1,x^3)的近似图形(绿色线段部分)对原图形(红色线段部分)近似效果不好,说明我们取的X中的点太少了,此时我们增加一个点来重新计算,那这个点就是我们求出来的最优解(x^0),记为X新的子集(X^1)=(X^0)U{(x^0)},再重复上面的计算,解
- max θ
- s.t. θ≤ f(x)+(λ^T)g(x)+(μ^T)h(x),∀x∈(X^1)
- λ≥0
以此不断反复求解,直到有1)或者2)两种情况的任一种发生,算法终止。
割平面法又称为外逼近算法
- 选取X的非空子集(X^1),其中(X^1)包含有限个元素,令k=1。
- 求解线性规划问题
-
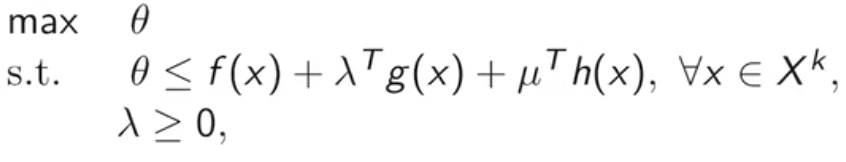
1. 记最优解为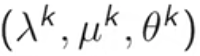
- 求解相应的子问题
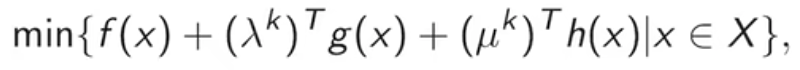
记其最优解为(x^k),最优值为

- 若(x^k)是原问题(P)的可行解,且

则算法终止,(x^k)和

分别是原问题(P)和对偶问题(D)的最优解,且最优值相等;若
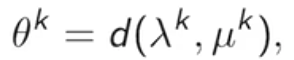
则算法终止,

即对偶问题(D)的最优解,且最优值为(θ^k).
- 令
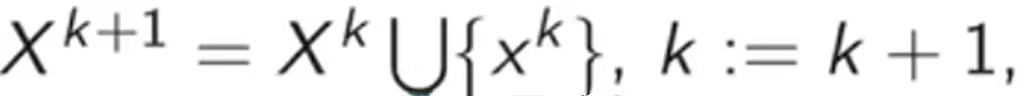
转step 2.
注意事项(Remark):
- X的子集合(X^1),包含(P)的一个可行点。如果(X^1)中的x是(P)的可行点,那么
- θ≤ f(x)+(λ^T)g(x)+(μ^T)h(x)≤f(x)
- 这里是为了给θ一个上界,否则θ很容易直接取到∞
- X包含了无穷个点,(X^1)中的点如果取的不是特别好的话,会产生非常糟糕的近似的效果,每一个点都不是起作用的点,那么算法会一直循环,意味着每一次加一个线性不等式进去,规模会越来越大,计算成本会越来越高。则我们需要在(X^k)中去掉多余的点,即在线性规划中去掉多余的线性不等式。
- 割平面
-
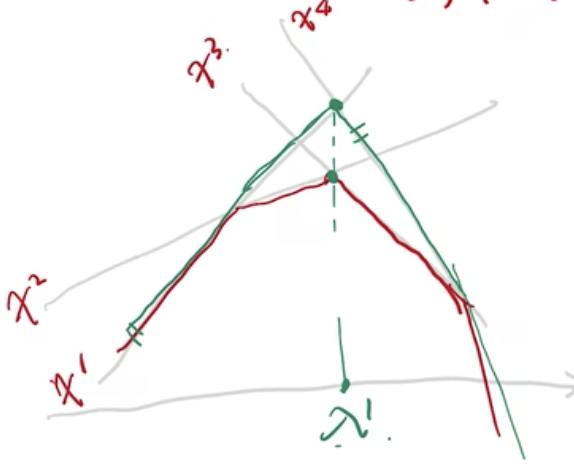
1. 在上图中,X包含四个点X={\(x^1,x^2,x^3,x^4\)},子集\(X^1\)={\(x^1,x^4\)},我们的线性规划问题是要对红色图形求最大,由\(X^1\)求出来的,就是上方的绿点,记为\(θ^1\),而真正的最优解d(\(λ^1\))(红色线段相交的绿点,由于是二维平面图形,这里不考虑μ,只考虑λ), d(\(λ^1\))≠\(θ^1\)。此时算法没有停止,需要继续往里面加条件,假设我们现在加进去的是\(x^2\)点,\(X^2\)={\(x^1,x^2,x^4\)}
2. 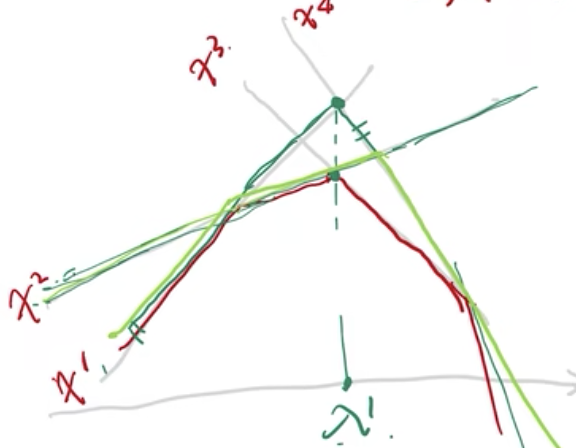
1. 上图中,浅绿色的部分是新添加了\(x^2\)后产生的图形,我们会发现\(X^2\)会比之前的\(X^1\)对于原函数的近似来的更好,割掉了\(θ^1\),所以这个方法叫割平面法,又称外逼近方法。在最优解附近会有不稳定性 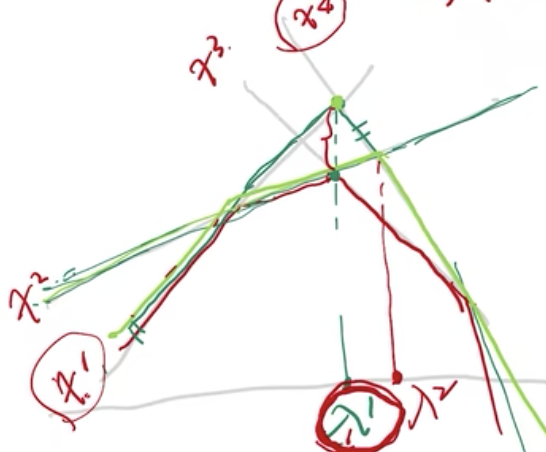
1. 在上图中,虽然 \(X^1\)={\(x^1,x^4\)}得到的\(θ^1\)≠ d(\(λ^1\)),没有重合,近似效果不好,我们将\(θ^1\)排除掉了,但其实\(λ^1\)就是我们要找的真正的最优解,此时我们就会发现割平面法一个很明显的缺点,就是在最优解到位置是无法去判断最优解的最优性的,算法流程当中是看近似效果的好坏,函数值是否相等,但很可能在迭代过程中已经找到了最优解或者很接近最优解,重新增加一个割平面的时候,很容易将找到的点离最优解拉扯的很远。如上图中\(λ^1\)是最优解,我们加入了\(x^2\)后找到的\(λ^2\),就偏离了最优解\(λ^1\),还可能偏离的还非常远。有一种方式——正则化方法可以克服这种不稳定性,就是增加一个惩罚项
2. max θ-σ\(||(λ,μ)^T-(λ^k,μ^k)^T||\_2^2\)
3. σ是惩罚项的系数,σ>0,其实就是希望在新的割平面同时,(\(λ^k,μ^k\))不要离当前的(λ,μ)特别远,要尽可能的小。腾讯云开发者

扫码关注腾讯云开发者
领取腾讯云代金券
Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号:粤B2-20090059 深公网安备号 44030502008569
腾讯云计算(北京)有限责任公司 京ICP证150476号 | 京ICP备11018762号 | 京公网安备号11010802020287
Copyright © 2013 - 2025 Tencent Cloud.
All Rights Reserved. 腾讯云 版权所有